Question

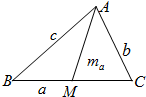如图：在△ABC中，角A，B，C的对边分别为a，b，c
（Ⅰ） 若BC边上的中点为M，且AM=m_a，求证：m_a=

1

2

2(b2+c2)-a2

；
（Ⅱ） 若△ABC是锐角三角形，且a=2bsinA．求u=cosA+sinC的取值范围．

Answer 1

考点：余弦定理的应用

专题：综合题,解三角形

分析：（Ⅰ）利用余弦定理，结合∠AMB+∠AMC=π⇒cos∠AMB+cos∠AMC=0，即可证明结论；
（Ⅱ）先确定A的范围，再化简u=cosA+sinC，即可求出结论．

解答： （Ⅰ） 证明：在△AMB中：c2=

m

2 a

+(

a

2

)2-2ma•

a

2

•cos∠AMB①
在△AMC中：b2=

m

2 a

+(

a

2

)2-2ma•

a

2

•cos∠AMC②
∵∠AMB+∠AMC=π⇒cos∠AMB+cos∠AMC=0，
∴①+②⇒b2+c2=2

m

2 a

+

a2

2

⇒ma=

1

2

2(b2+c2)-a2

（Ⅱ）解：a=2bsinA⇒sinA═2sinBsinA⇒sinB=

1

2

，
又△ABC为锐角三角形，
故B=

π

6

．从而C=π-

π

6

-A=

5π

6

-A．
∴u=cosA+sinC=cosA+sin(

5π

6

-A)=cosA+

1

2

cosA+

3

2

sinA=

3

2

cosA+

3

2

sinA=

3

sin(A+

π

3

)．
∵

0＜A＜ π 2 0＜ 5π 6 -A＜ π 2

?

π

3

＜A＜

π

2

，
∴

2π

3

＜A+

π

3

＜

5π

6

⇒

1

2

＜sin(A+

π

3

)＜

3

2

．
故u∈(

3

2

，

3

2

)．

点评：本题考查余弦定理的应用，考查三角函数的化简，考查学生分析解决问题的能力，属于中档题．