题目内容
已知△ABC的内角A,B,C所对的边分别为a,b,c.它的外接圆半径为6.∠B,∠C和△ABC的面积S满足条件:S=a2-(b-c)2且sinB+sinC=
.
(1)求sinA;
(2)求△ABC面积S的最大值.
| 4 |
| 3 |
(1)求sinA;
(2)求△ABC面积S的最大值.
考点:余弦定理的应用
专题:计算题,解三角形
分析:(1)△ABC的面积S满足条件:S=a2-(b-c)2 从而求出sinA=4(1-cosA)即可解得sinA的值;
(2)sinB+sinC=
.外接圆半径为6从而可求得b+c=16,故S=
bcsinA=
bc,当b=c=8时,S最大=
.
(2)sinB+sinC=
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 17 |
| 256 |
| 17 |
解答:
解:(1)S=a2-b2-c2+2bc
=2bc-2bccosA
=2bc(1-cosA).
又S=
bcsinA
∴2bc(1-cosA)=
bcsinA⇒sinA=4(1-cosA)
联立得:
得:16(1-cosA)2+cos2A=1⇒(17cos2A-15)(cosA-1)=0
∵0<A<π,
∴cosA-1≠1
∴cosA=
从而得:sinA=
(2)S=
bcsinA=
bc
∵sinB+sinC=
,
∴
+
=
∵R=6,
∴b+c=16
∴S=
bc=
b(16-b)=-
(b2-16b)=-
(b-8)2+
∴当b=c=8时,S最大=
.
=2bc-2bccosA
=2bc(1-cosA).
又S=
| 1 |
| 2 |
∴2bc(1-cosA)=
| 1 |
| 2 |
联立得:
|
得:16(1-cosA)2+cos2A=1⇒(17cos2A-15)(cosA-1)=0
∵0<A<π,
∴cosA-1≠1
∴cosA=
| 15 |
| 17 |
| 8 |
| 17 |
(2)S=
| 1 |
| 2 |
| 4 |
| 17 |
∵sinB+sinC=
| 4 |
| 3 |
∴
| b |
| 2R |
| c |
| 2R |
| 4 |
| 3 |
∵R=6,
∴b+c=16
∴S=
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| 256 |
| 17 |
∴当b=c=8时,S最大=
| 256 |
| 17 |
点评:本题主要考察了正弦定理,余弦定理,二次函数的图象和性质以及三角形面积公式的综合应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在数列{an}中,a1=2,an+1=an+ln(1+
),则an=( )
| 1 |
| n |
| A、2+ln n |
| B、2+(n-1)ln n |
| C、2+n ln n |
| D、1+n+ln n |
(x
-y
)6的展开式中x4y5的系数为( )
| y |
| x |
| A、20 | B、-20 |
| C、-15 | D、15 |
在区间(-∞,0)上为增函数的是( )
| A、y=-2x | ||
B、y=
| ||
| C、y=-x2 | ||
| D、y=|x| |
由y=ex、x轴、y轴及直线x=2围成的封闭图形的面积为( )
| A、e2 |
| B、e2-1 |
| C、e2+1 |
| D、e2ln2-1 |
函数y=cos(
x+
)是( )
| 1 |
| 2 |
| π |
| 2 |
| A、周期为2π的偶函数 |
| B、周期为4π的奇函数 |
| C、周期为4π的偶函数 |
| D、周期为π的奇函数 |
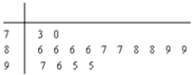 某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):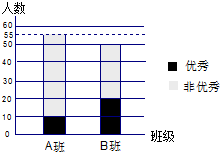 中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.
中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.