题目内容
若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为( )
| A、5或8 | B、-1或5 |
| C、-1或-4 | D、-4或8 |
考点:带绝对值的函数,函数最值的应用
专题:选作题,不等式
分析:分类讨论,利用f(x)=|x+1|+|2x+a|的最小值为3,建立方程,即可求出实数a的值.
解答:
解:-
<-1时,x<-
,f(x)=-x-1-2x-a=-3x-a-1>
-1;
-
≤x≤-1,f(x)=-x-1+2x+a=x+a-1≥
-1;
x>-1,f(x)=x+1+2x+a=3x+a+1>a-2,
∴
-1=3或a-2=3,
∴a=8或a=5,
a=5时,
-1<a-2,故舍去;
-
≥-1时,x<-1,f(x)=-x-1-2x-a=-3x-a-1>2-a;
-1≤x≤-
,f(x)=x+1-2x-a=-x-a+1≥-
+1;
x>-
,f(x)=x+1+2x+a=3x+a+1>-
+1,
∴2-a=3或-
+1=3,
∴a=-1或a=-4,
a=-1时,-
+1<2-a,故舍去;
综上,a=-4或8.
故选:D.
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
-
| a |
| 2 |
| a |
| 2 |
x>-1,f(x)=x+1+2x+a=3x+a+1>a-2,
∴
| a |
| 2 |
∴a=8或a=5,
a=5时,
| a |
| 2 |
-
| a |
| 2 |
-1≤x≤-
| a |
| 2 |
| a |
| 2 |
x>-
| a |
| 2 |
| a |
| 2 |
∴2-a=3或-
| a |
| 2 |
∴a=-1或a=-4,
a=-1时,-
| a |
| 2 |
综上,a=-4或8.
故选:D.
点评:本题主要考查了函数的值域问题.解题过程采用了分类讨论的思想,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
执行如图所示的程序框图,若输入的x,t均为2,则输出的S=( )


| A、4 | B、5 | C、6 | D、7 |
函数f(x)=ln(x2-x)的定义域为( )
| A、(0,1) |
| B、[0,1] |
| C、(-∞,0)∪(1,+∞) |
| D、(-∞,0]∪[1,+∞) |
设向量
,
满足|
+
|=
,|
-
|=
,则
•
=( )
| a |
| b |
| a |
| b |
| 10 |
| a |
| b |
| 6 |
| a |
| b |
| A、1 | B、2 | C、3 | D、5 |
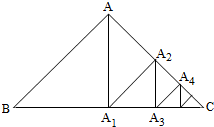 如图,在等腰直角三角形ABC中,斜边BC=2
如图,在等腰直角三角形ABC中,斜边BC=2