题目内容
F1、F2是椭圆
+y2=1的左、右焦点,点P在椭圆上运动,则
•
的最大值是 .
| x2 |
| 4 |
| PF1 |
| PF2 |
考点:椭圆的简单性质
专题:向量与圆锥曲线
分析:利用参数方程,设出点P的坐标,求出
•
的解析式,利用三角函数求出最大值.
| PF1 |
| PF2 |
解答:
解:在椭圆
+y2=1中,
a=2,b=1,∴c=
;
∴焦点F1(-
,0),F2(
,0);
设P满足
,θ∈[0,2π);
∴
•
=(2cosθ+
,sinθ)•(2cosθ-
,sinθ)
=(2cosθ+
)(2cosθ-
)+sin2θ
=4cos2θ-3+sin2θ=3cos2θ-2≤1,
当θ=0时,“=”成立.
故答案为:1.
| x2 |
| 4 |
a=2,b=1,∴c=
| 3 |
∴焦点F1(-
| 3 |
| 3 |
设P满足
|
∴
| PF1 |
| PF2 |
| 3 |
| 3 |
=(2cosθ+
| 3 |
| 3 |
=4cos2θ-3+sin2θ=3cos2θ-2≤1,
当θ=0时,“=”成立.
故答案为:1.
点评:本题考查了向量与圆锥曲线的应用问题,解题时应利用参数方程,设出点P的坐标,求出目标函数的最值,是中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知(1+x)8=a0+a1x+a2x2+…+a8x8,则a1+a2+…+a8的值是( )
| A、28 |
| B、28-1 |
| C、26-1 |
| D、26 |
设直线过点(0,a),其斜率为1,且与圆x2+y2=4相切,则a的值为( )
| A、±4 | ||
B、±2
| ||
| C、4x+2y=5 | ||
| D、4x-2y=5 |

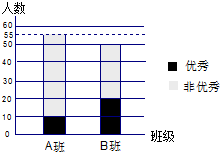 中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.
中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.