题目内容
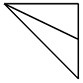
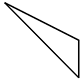
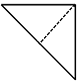
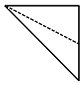
18.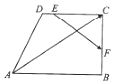 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=3,BC=DC=2,若E,F分别是线段DC和BC上的动点,则$\overrightarrow{AC}•\overrightarrow{EF}$的取值范围是[-4,6].
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=3,BC=DC=2,若E,F分别是线段DC和BC上的动点,则$\overrightarrow{AC}•\overrightarrow{EF}$的取值范围是[-4,6].
分析 依题意,设$\overrightarrow{EC}$=λ$\overrightarrow{AB}$(0≤λ≤$\frac{2}{3}$),$\overrightarrow{CF}$=μ$\overrightarrow{BC}$(-1≤μ≤0),由$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$,$\overrightarrow{EF}$=$\overrightarrow{EC}$+$\overrightarrow{CF}$,可求得$\overrightarrow{AC}•\overrightarrow{EF}$=($\overrightarrow{AB}$+$\overrightarrow{BC}$)•($\overrightarrow{EC}$+$\overrightarrow{CF}$)=λ${\overrightarrow{AB}}^{2}$+μ${\overrightarrow{BC}}^{2}$=9λ+4μ;再由0≤λ≤$\frac{2}{3}$,-1≤μ≤0,即可求得-4≤9λ+4μ≤6,从而可得答案.
解答 解:∵AB∥DC,∠ABC=90°,AB=3,BC=DC=2,且E,F分别是线段DC和BC上的动点,
∴$\overrightarrow{EC}$=λ$\overrightarrow{AB}$(0≤λ≤$\frac{2}{3}$),
$\overrightarrow{CF}$=μ$\overrightarrow{BC}$(-1≤μ≤0),
又$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$,$\overrightarrow{EF}$=$\overrightarrow{EC}$+$\overrightarrow{CF}$,
∴$\overrightarrow{AC}•\overrightarrow{EF}$=($\overrightarrow{AB}$+$\overrightarrow{BC}$)•($\overrightarrow{EC}$+$\overrightarrow{CF}$)
=($\overrightarrow{AB}$+$\overrightarrow{BC}$)•(λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$)
=λ${\overrightarrow{AB}}^{2}$+μ${\overrightarrow{BC}}^{2}$
=9λ+4μ.
∵0≤λ≤$\frac{2}{3}$,∴0≤9λ≤6①,
又-1≤μ≤0,∴-4≤4μ≤0②,
①+②得:-4≤9λ+4μ≤6.
即$\overrightarrow{AC}•\overrightarrow{EF}$的取值范围是[-4,6],
故答案为:[-4,6].
点评 本题考查平面向量数量积的坐标运算,设$\overrightarrow{EC}$=λ$\overrightarrow{AB}$(0≤λ≤$\frac{2}{3}$),$\overrightarrow{CF}$=μ$\overrightarrow{BC}$(-1≤μ≤0),并求得$\overrightarrow{AC}•\overrightarrow{EF}$=9λ+4μ是关键,考查平面向量加法的三角形法与共线向量基本定理的应用,考查运算求解能力,属于中档题.

| A. | 2x>2y | B. | lgx>lgy | C. | $\frac{1}{x}>\frac{1}{y}$ | D. | x2>y2 |
| A. | 偶函数且它的图象关于点(π,0)对称 | |
| B. | 偶函数且它的图象关于点$(\frac{3π}{2},0)$对称 | |
| C. | 奇函数且它的图象关于点(π,0)对称 | |
| D. | 奇函数且它的图象关于点$(\frac{3π}{2},0)$对称 |
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是( )
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是( )| A. | f(x)=2sin(πx+$\frac{π}{6}$) | B. | f(x)=2sin(2πx+$\frac{π}{6}$) | C. | f(x)=2sin(πx+$\frac{π}{3}$) | D. | f(x)=2sin(2πx+$\frac{π}{3}$) |