题目内容
已知全集U=R,非空集合A={x|
<0},B={x|(x-a)(x-a-4)<0}.
(1)当a=-
时,求A∩B;
(2)命题p:x∈A,命题q:x∈B,若¬p是¬q的必要不充分条件,求实数a的取值范围.
| x-2 |
| x-3 |
(1)当a=-
| 3 |
| 2 |
(2)命题p:x∈A,命题q:x∈B,若¬p是¬q的必要不充分条件,求实数a的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:(1)当a=-
时求出集合A,B,根据集合的基本运算即可.
(2)然后利用¬p是¬q的必要不充分条件,即q是p的必要不充分条件,进行确定范围.
| 3 |
| 2 |
(2)然后利用¬p是¬q的必要不充分条件,即q是p的必要不充分条件,进行确定范围.
解答:
解:(1)当a=-
时,B={x|(x-a)(x-a-4)<0}={x|-
<x<
},A={x|
<0}={x|2<x<3},
则A∩B={x|2<x<
}.
(2)B={x|(x-a)(x-a-4)<0}={x|a<x<a+4}.
因为¬p是¬q的必要不充分条件,即q是p的必要不充分条件,
则A⊆B,
则
,
即
,
解得-1≤a≤2.
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| x-2 |
| x-3 |
则A∩B={x|2<x<
| 5 |
| 2 |
(2)B={x|(x-a)(x-a-4)<0}={x|a<x<a+4}.
因为¬p是¬q的必要不充分条件,即q是p的必要不充分条件,
则A⊆B,
则
|
即
|
解得-1≤a≤2.
点评:本题主要考查充分条件和必要条件的应用,将¬p是¬q的必要不充分条件转化为q是p的必要不充分条件,是解决本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
函数y=logax (0<a<1)的图象大致是( )
A、 |
B、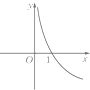 |
C、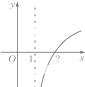 |
D、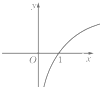 |
函数f(x)=ex+5x-5零点所在的区间为( )
| A、(-2,-1) |
| B、(-1,0) |
| C、(0,1) |
| D、(1,2) |
下列函数在区间(-∞,0)上为增函数的是( )
A、y=
| ||
B、y=
| ||
| C、y=-x2-2x-1 | ||
| D、y=1+x2 |
“方程
+
=1表示焦点在y轴上的椭圆”是“n>m>0”的( )
| x2 |
| m2 |
| y2 |
| n2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知等比数列{an}中,
=2,a4=8,则a6=( )
| a2+a3 |
| a1+a2 |
| A、31 | B、32 | C、63 | D、64 |
 已知正四棱锥(底面是正方形,顶点在底面的投影是底面的中心)P-ABCD如图.
已知正四棱锥(底面是正方形,顶点在底面的投影是底面的中心)P-ABCD如图.