Question

已知正四棱锥（底面是正方形，顶点在底面的投影是底面的中心）P-ABCD如图．
（1）设AB中点为M，PC中点为N，证明：MN∥平面PAD；
（2）若其正视图是一个边长分别为

3

、

3

、2的等腰三角形，求其表面积S、体积V．

Answer 1

考点：直线与平面平行的判定,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（1）取PD得中点为F，利用三角形的中位线的性质证明AM和 NF平行且相等，可得AMNF为平行四边形，AF∥MN．再利用直线和平面平行的判定定理证明MN∥平面PAD．
（2）解设CD中点为E，则正四棱锥的正视图为三角形PME．依题意，PM=

3

、PE=

3

、ME=2，由此求得四棱锥的表面积S、体积V．

解答： （1）证明：取PD得中点为F，由AB中点为M，PC中点为N，可得NF为△PCD的中位线，故有NF∥CD，NF=

1

2

CD．
再根据正四棱锥P-ABCD中，AM∥CD，AM=

1

2

CD，可得AM和 NF平行且相等，故AMNF为平行四边形，∴AF∥MN．
由于AF?平面PAD，MN?平面PAD，∴MN∥平面PAD．

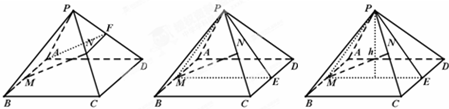
（2）解设CD中点为E，则正四棱锥的正视图为三角形PME．
依题意，PM=

3

、PE=

3

、ME=2，
故几何体的表面积S=4×(

1

2

×2×

3

)+2×2=4

3

+4，
体积V=

1

3

×4×

( 3 )2-12

=

4 2

3

．

点评：本题主要考查直线和平面平行的判定定理的应用，几何体的三视图，求棱锥的表面积和体积，属于基础题．