题目内容
2.已知不等式组$\left\{\begin{array}{l}{y-1≥0}\\{x+y-4≤0}\\{y-1≤k(x-1)}\end{array}\right.$(k>0)表示的平面区域为D,若?(x,y)∈D,$\frac{y}{{x}^{2}}$≤1恒成立,则实数k的取值范围是(0,1].分析 如图所示,题中不等式组表示的平面区域为图中直线AB上方、直线BC的下方,且y-1=k(x-1)下方的区域.由此将直线y-1=k(x-1)绕A(1,1)旋转,观察斜率的变化并计算$\frac{y}{{x}^{2}}$的值,可得实数k的取值范围.
解答 解:如图示: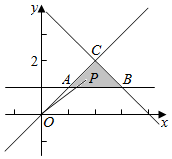 ,
,
根据题意,直线y-1=k(x-1)经过定点A(1,1)
不等式组表示的平面区域为直线AB上方、直线BC的下方,且y-1=k(x-1)下方的区域
∵$\frac{y}{{x}^{2}}$的最大值为1,即当点P与点A重合时$\frac{y}{{x}^{2}}$有最大值
∴直线y-1=k(x-1)绕A点顺时针旋转,且满足斜率大于0时,符合题意,
因此斜率的范围为(0,1],即实数k的取值范围是(0,1].
故答案为:(0,1].
点评 本题给出二元一次不等式组,求目标函数的最值和参数的取值范围,着重考查了二元一次不等式组表示的平面区域和直线的斜率等知识,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
12.己知集合M={x|-x2-x+6>0},N={x|lgx≥0},则M∩N=( )
| A. | (-2,∞) | B. | [1,2) | C. | (-2,-1] | D. | (-2,3) |