题目内容
10.已知△ABC外接圆O的半径为2,且$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$,|$\overrightarrow{AB}$|=|$\overrightarrow{AO}$|,则$\overrightarrow{CA}•\overrightarrow{CB}$=12.分析 运用平面向量的三角形法则,以及外心的特点,可得O为BC的中点,三角形ABC为直角三角形,
再由勾股定理和向量的数量积定义,即可求出结果.
解答 解:如图所示,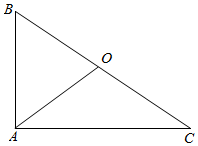
△ABC的外接圆的半径为2,且$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$,
∴($\overrightarrow{OB}$-$\overrightarrow{OA}$)+($\overrightarrow{OC}$-$\overrightarrow{OA}$)=2$\overrightarrow{AO}$,
∴$\overline{OB}$+$\overrightarrow{OC}$=2$\overrightarrow{AO}$+2$\overrightarrow{OA}$=$\overrightarrow{0}$,
∴O为BC的中点,
即AB⊥AC;
又|$\overrightarrow{AB}$|=|$\overrightarrow{AO}$|,
∴△ABO为等边三角形,且边长为2,
由勾股定理得,AC=$\sqrt{{BC}^{2}{-AB}^{2}}$=2$\sqrt{3}$,
则$\overrightarrow{CA}$•$\overrightarrow{CB}$=|$\overrightarrow{CA}$|•|$\overrightarrow{CB}$|•cos∠ACB=2$\sqrt{3}$×4×$\frac{\sqrt{3}}{2}$=12.
故答案为:12.
点评 本题考查了平面向量的三角形法则和数量积的定义应用问题,也考查了三角形的外心概念与勾股定理的运用,是基础题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目