题目内容
在△ABC中，已知sinA•sinB•cosC=sinA•sinC•cosB+sinB•sinC•cosA，若a，b，c分别是角A，B，C所对的边，则
的最大值为 ．
| ab |
| c2 |
考点：正弦定理
专题：
分析：利用正弦定理、余弦定理、基本不等式即可得出．
解答：
解：由sinA•sinB•cosC=sinA•sinC•cosB+sinB•sinC•cosA，
利用正弦定理可得：abcosC=accosB+bccosA，
由余弦定理可得：a2+b2-c2=a2+c2-b2+b2+c2-a2，
化为a2+b2=3c2，
∴3c2≥2ab，化为
≤
，当且仅当a=b时取等号．
故答案为：
．
利用正弦定理可得：abcosC=accosB+bccosA，
由余弦定理可得：a2+b2-c2=a2+c2-b2+b2+c2-a2，
化为a2+b2=3c2，
∴3c2≥2ab，化为
| ab |
| c2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题考查了正弦定理、余弦定理、基本不等式，属于中档题．
练习册系列答案
相关题目
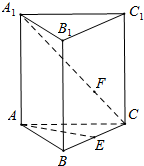如图，已知正三棱柱ABC-A1B1C1的各棱长都是4，E是BC的中点，动点F在线段CA1上，且不与点C、A1重合．
如图所示，四边形ABEF和ABCD都是直角梯形，∠BAD=∠FAB=90°，BC