题目内容
20.已知过点M($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)的椭圆C的中心在坐标原点,对称轴为坐标轴,若这个椭圆的一个焦点为F(-1,0).(1)求椭圆C的方程;
(2)过点F(-1,0)、倾斜角为$\frac{π}{4}$的直线l交椭圆C于两点,求这两点间的距离.
分析 (1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得c=1,代入点M,解方程可得a,b,进而得到椭圆方程;
(2)运用点斜式方程可得直线l的方程,代入椭圆方程,求得交点,由两点的距离公式,计算即可得到所求值.
解答 解:(1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=1,a2-b2=1,
又$\frac{1}{2{a}^{2}}$+$\frac{3}{4{b}^{2}}$=1,
解方程可得a=$\sqrt{2}$,b=c=1,
则椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)由题意可得直线l的方程为y=x+1,
代入椭圆方程,可得3x2+4x=0,
解得x=0或-$\frac{4}{3}$,
即有交点为(0,1),(-$\frac{4}{3}$,-$\frac{1}{3}$),
则交点间的距离为$\sqrt{(0+\frac{4}{3})^{2}+(1+\frac{1}{3})^{2}}$=$\frac{4}{3}$$\sqrt{2}$.
点评 本题考查椭圆的方程的求法,考查点在椭圆上满足椭圆方程,同时考查直线和椭圆相交,运用两点的距离公式,属于基础题.

练习册系列答案
相关题目
8.一个几何体的三视图如图所示,俯视图为等边三角形,若其侧面积为12$\sqrt{3}$,则a是( )
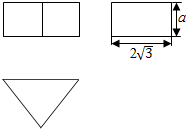

| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
5.某几何体的三视图如图所示,则该几何体的表面积为( )
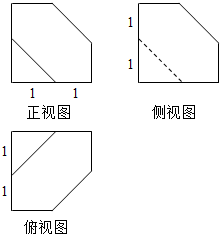

| A. | 1 | B. | 21+$\sqrt{3}$ | C. | 3$\sqrt{3}$+12 | D. | $\frac{3\sqrt{3}}{2}$+12 |
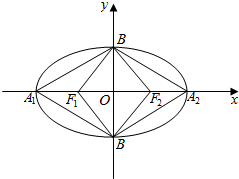 如图所示,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A1、A2、B1、B2、F1、F2分别是其左右顶点,上下顶点和左右焦点,四边形A1B1A2B2的面积是四边形B1F2B2F1面积的2倍.
如图所示,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A1、A2、B1、B2、F1、F2分别是其左右顶点,上下顶点和左右焦点,四边形A1B1A2B2的面积是四边形B1F2B2F1面积的2倍.
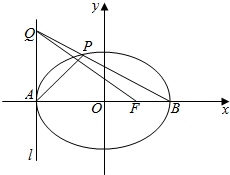 如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.
如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.