题目内容

设Γ={（x，y）|x2-y2=1，x＞0}，点M是坐标平面内的动点．若对任意的不同两点P，Q∈Γ，∠PMQ恒为锐角，则点M所在的平面区域（阴影部分）为（　　）
A、
B、
C、
D、
考点：二元一次不等式（组）与平面区域
专题：不等式的解法及应用
分析：根据双曲线的渐近线的夹角，利用数形结合即可．
解答： 解：双曲线的渐近线为y=±x，则两渐近线的夹角为90°，
若∠PMQ恒为锐角，
则点M所在的平面区域（阴影部分）为，
故选：B
点评：本题主要考查双曲线的渐近线的性质以及二元一次不等式表示平面区域，比较基础．
练习册系列答案
相关题目
若函数f（x）和g（x）满足：①在区间[a，b]上均有定义；②函数y=f（x）-g（x）在区间[a，b]上至少有一个零点，则称f（x）和g（x）在[a，b]上具有关系G．
（1）若f（x）=lgx，g（x）=3-x，试判断f（x）和g（x）在[1，4]上是否具有关系G，并说明理由；
（2）若f（x）=2|x-2|+1和g（x）=mx2在[1，4]上具有关系G，求实数m的取值范围．
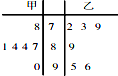甲乙两同学在高二年级的6次数学测验成绩（满分100分）如图茎叶图所示，则下列说法正确的是（　　）
A、甲乙同学的平均成绩相同，但是甲同学的成绩比乙稳定
B、甲乙同学的平均成绩相同，但是乙同学的成绩比甲稳定
C、甲同学的平均成绩比乙同学好，但是乙同学的成绩比甲稳定
D、乙同学的平均成绩比甲同学好，但是甲同学的成绩比乙稳定
已知圆C：x2+y2+Dx+Ey+3=0，圆C关于直线x+y-1=0对称，圆心在第二象限，半径为
2
．
（1）求圆C的方程；
（2）已知不过原点的直线l与圆C相切，且与x轴、y轴上的截距相等，求直线l的方程．
设i为虚数单位，则复数
3-4i
i
=（　　）
A、-4-3iB、-4+3i
C、4+3iD、4-3i
下列命题中：
①函数f（x）=
1
x
在定义域内为单调递减函数
②函数f（x）=x+
a
x
（x＞0）的最小值为2
a

③已知定义在R上周期为4的函数f（x）满足f（2-x）=f（2+x），则f（x）一定为偶函数
④已知函数f（x）=ax3+bx2+cx+d（a≠0），则a+b+c=0是f（x）有极值的必要不充分条件；
⑤已知函数f（x）=x-sinx，若a+b＞0，则f（a）+f（b）＞0．
其中正确命题的序号为
 
（写出所有正确命题的序号）．
二阶矩阵M对应的变换TM将曲线x2+x-y+1=0变为曲线2y2-x+2=0．求M-1．
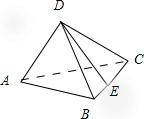在四面体ABCD中，已知
AB
=
b
，
AD
=
a
，
AC
=
c
，
BE
=
1
2
EC
，则
DE
=（　　）
A、-
a
+
2
3
b
+
1
3
c
B、
a
+
2
3
b
+
1
3
c
C、
a
-
2
3
b
+
1
3
c
D、
2
3
a
-
b
+
1
3
c
已知函数f（x）=asin（
π
2
+ωx）•sin（ωx+
π
3
）（a≠0，ω＞0，x∈R），函数y=f（x）的最小正周期为π．
（1）求ω的值；
（2）将函数 f（x）的图象向右平移
π
3
个单位后得到函数y=g（x）的图象，求y=g（x）在[0，
π
2
]上的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网