题目内容
函数f（x）=（x-1）2+2，x∈[0，2）的值域是 ．
考点：函数的值域
专题：函数的性质及应用
分析：求出函数的对称轴，利用二次函数的性质写出结果即可．
解答：
解：函数f（x）=（x-1）2+2，x∈[0，2），
函数的对称轴为x=1，开口向上，函数的最小值为f（1）=2，函数的最大值为：f（0）=3．
函数的值域为[2，3]．
故答案为：[2，3]．
函数的对称轴为x=1，开口向上，函数的最小值为f（1）=2，函数的最大值为：f（0）=3．
函数的值域为[2，3]．
故答案为：[2，3]．
点评：本题考查函数的值域，二次函数的基本性质的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
函数y=
cos2x的图象可以看作是把函数y=
cos（2x+
）图象（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
甲、乙两名运动员在某项测试中的8次成绩如下，
甲：8，9，14，15，15，16，21，22
乙：7，8，13，15，15，17，22，23
则下面说法正确的是（ ）
甲：8，9，14，15，15，16，21，22
乙：7，8，13，15，15，17，22，23
则下面说法正确的是（ ）
| A、甲的平均数和方差都比乙的大 |
| B、甲、乙的平均数相等，但甲的方差比乙的方差小 |
| C、甲、乙的平均数相等，但甲的方差比乙的方差大 |
| D、甲的平均数小于乙的平均数，但甲的方差大于乙的方差 |
（1）画出函数f（x）=|x|（x-4）的图象；
若f（x）是R上的奇函数，在[0，+∞）上图象如图所示，则满足f（x-1）＞0的x的集合是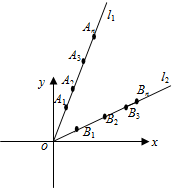
已知直线l1：y=3x，l2：y=