Question

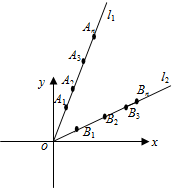已知直线l₁：y=3x，l₂：y=

1

2

x，如图所示，在第一象限内，在l₁上从左至右，从下至上依次取点A₁，A₂，A₃，…，A_n，在l₂上从左至右，从下至上依次取点B₁，B₂，B₃，…，B_n，若记S △A1OB1=S₁，S △A2OB2=S₂，…，S △AnOBn=S_n，…．
（1）求∠A₁OB₁的大小；
（2）再记S △A1OB2=S₁′，S △A2OB1=S₂′，试比较S₁+S₂与S₁′+S₂′的大小关系．
（3）若S₁=1，且S_n+1=1+

1

n

（S₁+S₂+…+S_n），n∈N^*，求四边形A_n+1B_n+1B_nA_n（n∈N^*）的面积．

Answer 1

考点：数列的应用,数列的求和

专题：等差数列与等比数列

分析：（1）运用两条直线的夹角公式求解，（2）利用三角形的面积公式，

1

2

absinθ，（3）两个三角形面积的差，利用递推关系式求解，归纳总结的出答案．

解答： 解：（1）∵直线l₁：y=3x，l₂：y=

1

2

x，∴tan∠A₁OB₁=

3- 1 2

1+3× 1 2

=1，
∵∈（0，π），∴∠A₁OB₁=

π

4

，
（2）S △A1OB1=S₁=

1

2

|OA₁||OB₁|×

2

2

=

2

4

×|OA₁|OB₁|，|S △A2OB2=S₂=

2

4

×|OA₂||OB₂|，
S △A1OB2=S₁′=

2

4

×|OA₁|OB₂|，S △A2OB1=S₂′=

2

4

×|OA₂||OB₁|
S₁+S₂-（S₁′+S₂′）=（|OA₁|-|OA₂|）（|OB₁|-|OB₂|）
|OA₁|＜|OA₂|，|OB₁|＜|OB₂|，
（|OA₁|-|OA₂|）（|OB₁|-|OB₂|）＞0，
S₁+S₂＞S₁′+S₂′
（3）S₁=1，且S_n+1=1+

1

n

（S₁+S₂+…+S_n），n∈N^*，
∴S₂=2，S₃=

5

2

，S₄=

17

6

，S₅=

37

12

，
四边形A₁A₂B₁B₂的面积为2-1=1；
四边形A₂A₃B₂B₃的面积为

5

2

-2=

1

2

；
四边形A₃A₄B₃B₄的面积为

17

6

-

5

2

=

1

3

；
四边形A₄A₅B₄B₅的面积为

37

12

-

17

6

=

1

4

；
归纳推理得四边形A_n+1B_n+1B_nA_n（n∈N^*）的面积为：

1

n

，

点评：本题考查了学生的归纳猜测能力，运算能力，化简能力，学会数学知识的融合．