题目内容
已知数列{an}的前n项和Sn=n2
(1)求数列{an}的通项公式,并证明{an}为等差数列;
(2)记bn=
,Tn=b1+b2+…+bn,若?n∈N*,Tn>m,求m的取值范围.
(1)求数列{an}的通项公式,并证明{an}为等差数列;
(2)记bn=
| 1 |
| anan+1 |
考点:数列与不等式的综合,等差关系的确定
专题:综合题,等差数列与等比数列
分析:(1)根据数列{an}的前n项和Sn,表示出数列{an}的前n-1项和Sn-1,两式相减即可求出此数列的通项公式,然后把n=1代入也满足,故此数列为等差数列,求出的an即为通项公式;
(2)利用裂项法求和,再根据数列的单调性,即可求m的取值范围.
(2)利用裂项法求和,再根据数列的单调性,即可求m的取值范围.
解答:
解:(1)当n=1时,S1=12=1,
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
又n=1时,a1=2-1=1,满足通项公式,
∴此数列为等差数列,其通项公式为an=2n-1;…4分
∵an+1-an=2,
∴{an}为等差数列;…6分
(2)bn=
=
(
-
),
Tn=b1+b2+…+bn=
(1-
+
-
+…+
-
)=
(1-
),…10分
Tn=
(1-
)在n∈N*上单调递增,所以n=1时(Tn)min=
∴m的取值范围是(-∞,
)…14分.
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
又n=1时,a1=2-1=1,满足通项公式,
∴此数列为等差数列,其通项公式为an=2n-1;…4分
∵an+1-an=2,
∴{an}为等差数列;…6分
(2)bn=
| 1 |
| anan+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
Tn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
Tn=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 3 |
∴m的取值范围是(-∞,
| 1 |
| 3 |
点评:此题考查了等差数列的通项公式,考查裂项法,灵活运用an=Sn-Sn-1求出数列的通项公式是关键.

练习册系列答案
相关题目
在复平面内与复数z=
所对应的点关于虚轴对称的点为A,则A对应的复数为( )
| 5i |
| 1+2i |
| A、1+2i | B、1-2i |
| C、-2+i | D、2+i |
集合{x∈N|x-3<2},用列举法表示是( )
| A、{0,1,2,3,4} |
| B、{1,2,3,4} |
| C、{0,1,2,3,4,5} |
| D、{1,2,3,4,5} |
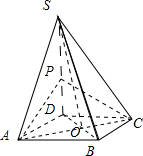 如图,四棱锥S-ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.
如图,四棱锥S-ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.