题目内容
已知异面直线a,b所成的角为θ,P为空间任意一点,过P作直线l,若l与a,b所成的角均为φ,有以下命题:
①若θ=60°,φ=90°,则满足条件的直线l有且仅有l条;
②若θ=60°,φ=30°,则满足条件的直线l有仅有l条;
③若θ=60°,φ=70°,则满足条件的直线l有且仅有4条;
④若θ=60°,φ=45°,则满足条件的直线l有且仅有2条;
上述4个命题中真命题有( )
①若θ=60°,φ=90°,则满足条件的直线l有且仅有l条;
②若θ=60°,φ=30°,则满足条件的直线l有仅有l条;
③若θ=60°,φ=70°,则满足条件的直线l有且仅有4条;
④若θ=60°,φ=45°,则满足条件的直线l有且仅有2条;
上述4个命题中真命题有( )
| A、l个 | B、2个 | C、3个 | D、4个 |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:如果a与b所成角为θ,过P点与a,b所成角都是φ的直线条数为:若φ<
,则为0条;若φ=
,则为1条;若
<φ<
,则为2条;若φ=
,则为3条;若
<φ<90°,则为4条;若φ=900,则为1条.
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| 180°-θ |
| 2 |
| 180°-θ |
| 2 |
| 180°-θ |
| 2 |
解答:
解:如果a与b所成角为θ,过P点与a,b所成角都是φ的直线条数为:
若φ<
,则为0条;若φ=
,则为1条;若
<φ<
,则为2条;
若φ=
,则为3条;若
<φ<90°,则为4条;
若φ=900,则为1条.
由此可知:
①若θ=60°,φ=90°,则满足条件的直线l有且仅有l条,是真命题;
②若θ=60°,φ=30°,则满足条件的直线l有仅有l条,是真命题;
③若θ=60°,φ=70°,则满足条件的直线l有且仅有4条,是真命题;
④若θ=60°,φ=45°,则满足条件的直线l有且仅有2条,是真命题.
故选:D.
若φ<
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| 180°-θ |
| 2 |
若φ=
| 180°-θ |
| 2 |
| 180°-θ |
| 2 |
若φ=900,则为1条.
由此可知:
①若θ=60°,φ=90°,则满足条件的直线l有且仅有l条,是真命题;
②若θ=60°,φ=30°,则满足条件的直线l有仅有l条,是真命题;
③若θ=60°,φ=70°,则满足条件的直线l有且仅有4条,是真命题;
④若θ=60°,φ=45°,则满足条件的直线l有且仅有2条,是真命题.
故选:D.
点评:本小题主要考查异面直线所成的角、异面直线所成的角的求法,以及射影等知识,考查空间想象能力、运算能力和推理论证能力,考查转化思想,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
设条件P:
>0,条件Q:|x-1|<1,则P是Q的( )
| x+2 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下表是降耗技术改造后生产甲产品过程中记录的产品x(吨)与相应生产耗能(吨标准煤)的几组相应数据.求出线性回归方程
=0.7x+0.35,则表中的m值为( )
 |
| y |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
| A、3 | B、4 | C、3.15 | D、4.5 |
已知集合M={x|
<-1},N={x|x2<-x},则( )
| 1 |
| x |
| A、M?N | B、M=N |
| C、M?N | D、M∩N=∅ |
抛物线y=3x2的焦点坐标是( )
A、(0,
| ||
B、(0,-
| ||
C、(0,-
| ||
D、(0,
|
设离散型随机变量X的概率分布列如下表:
则p等于( )
| X | 1 | 2 | 3 | 4 | ||||||
| P |
| p |
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
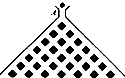 如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑道.黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是