题目内容
已知集合A={x|
≥1},B={x|y=
},则A∪B=( )
| 1 |
| x+1 |
| x2-1 |
| A、(-∞,1] |
| B、(-1,0)∪[1,+∞) |
| C、(-∞,0)∪[1,+∞) |
| D、(-∞,0]∪[1,+∞) |
考点:并集及其运算
专题:集合
分析:求出A中不等式的解集确定出A,求出B中x的范围确定出B,求出A与B的并集即可.
解答:
解:由A中不等式变形得:
-1≥0,即
≥0,
整理得:
≤0,即x(x+1)≤0,且x+1≠0,
解得:-1<x≤0,即A=(-1,0],
由B中y=
,得到x2-1≥0,即(x+1)(x-1)≥0,
解得:x≥1或x≤-1,即B=(-∞,-1]∪[1,+∞),
则A∪B=(-∞,0]∪[1,+∞).
故选:D.
| 1 |
| x+1 |
| 1-x-1 |
| x+1 |
整理得:
| x |
| x+1 |
解得:-1<x≤0,即A=(-1,0],
由B中y=
| x2-1 |
解得:x≥1或x≤-1,即B=(-∞,-1]∪[1,+∞),
则A∪B=(-∞,0]∪[1,+∞).
故选:D.
点评:此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
相关题目
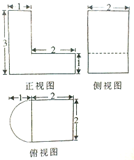
某几何体的三视图如图所示,则该几何体的体积为( )

A、4+
| ||
B、4+
| ||
C、4+
| ||
| D、4+π |
设集合U={x|x是小于5的正整数},A={1,2},则∁UA=( )
| A、{3,4,5} |
| B、{3,4} |
| C、{0,1,3,4} |
| D、{0,3,4,5} |
设条件P:
>0,条件Q:|x-1|<1,则P是Q的( )
| x+2 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知数列{cn}的通项是cn=
,则数列{cn}中的正整数项有( )项.
| 4n+31 |
| 2n-1 |
| A、1 | B、2 | C、3 | D、4 |
a,b∈R,下列不等式中一定成立的是( )
| A、若a>b,则a2>b2 | ||||
B、若a>b,则
| ||||
| C、若|a|>b,则a2>b2 | ||||
| D、若a>|b|,则a2>b2 |
sin(-
)的值为( )
| 25π |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|