题目内容
12.已知一个扇形的周长是12cm,(1)若扇形的圆心角α=300,求该扇形的半径
(2)当扇形半径为何值时,这个扇形的面积最大?别求出此时的圆心角.
分析 (1)设出扇形的半径,求出扇形的弧长,利用周长公式,求出半径.
(2)首先,设扇形的弧长,然后,建立关系式,求解S=$\frac{1}{2}$lR=-R2+6R,结合二次函数的图象与性质求解最值即可.
解答 解:(1)设扇形的半径为:R,扇形的圆心角α=300=$\frac{π}{6}$,
可得:2R+L=12,
所以2R+$\frac{π}{6}$R=12,
所以解得:R=$\frac{72}{12+π}$.
(2)设扇形的弧长为l,
∵l+2R=12,
∴S=$\frac{1}{2}$lR=$\frac{1}{2}$(12-2R)R
=-R2+6R
=9-(R-3)2,
∴当R=3时,扇形有最大面积9,
此时l=12-2R=6,α=$\frac{l}{R}$=2,
故当扇形的圆心角为2时,扇形有最大面积9.
点评 本题重点考查了扇形的面积公式、弧长公式、二次函数的最值等知识,熟练扇形的弧长公式以及扇形面积公式是关键,考查计算能力,属于基础题.

练习册系列答案
相关题目
3.已知命题p:关于x的函数y=x2-3ax+4在[1,+∞)上是增函数,命题q:关于x的函数y=(2a-1)x在[1,+∞)上是减函数.若“p且q”为真命题,则实数a的取值范围是( )
| A. | (-∞,$\frac{2}{3}$] | B. | (0,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{2}{3}$] | D. | ($\frac{1}{2}$,1) |
17.通过随机询问某校高二年级学生在购买食物时是否看营养说明,得到如下列联表:
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(b+d)(a+c)(c+d)}$,n=a+b+c+d
(1)写出x,y,z的值
(2)根据以上列联表,问有多大把握认为“性别在购买食物时看营养说明”有关?
(3)从女生中按是否看营养说明采取分层抽样,抽取容量为5的样本,再从这5名女生中随机选取两名作深度访谈.求选到看与不看营养说明的女生各一名的概率.
| 男生 | 女生 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | x | y |
| 总计 | 60 | z | 110 |
| P(K2≥K) | 0.10 | 0.05 | 0.01 | 0.005 |
| K | 2.706 | 3.841 | 6.635 | 7.879 |
(1)写出x,y,z的值
(2)根据以上列联表,问有多大把握认为“性别在购买食物时看营养说明”有关?
(3)从女生中按是否看营养说明采取分层抽样,抽取容量为5的样本,再从这5名女生中随机选取两名作深度访谈.求选到看与不看营养说明的女生各一名的概率.
4.${x^2}-{log_a}(x+1)<2x-1在(\frac{1}{2},1)$内恒成立,则a的取值范围是( )
| A. | $[{({\frac{3}{2}})^{-4}},1)$ | B. | $({({\frac{3}{2}})^{-4}},1)$ | C. | $(1,{({\frac{3}{2}})^4})$ | D. | $(1,{({\frac{3}{2}})^4}]$ |
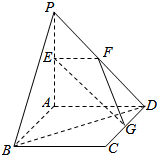 平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点
平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点 如图,在△ABC中,BC边上的中线AD长为3,且BD=2,$sinB=\frac{{3\sqrt{6}}}{8}$.
如图,在△ABC中,BC边上的中线AD长为3,且BD=2,$sinB=\frac{{3\sqrt{6}}}{8}$. 已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.
已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.