题目内容
17.通过随机询问某校高二年级学生在购买食物时是否看营养说明,得到如下列联表:| 男生 | 女生 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | x | y |
| 总计 | 60 | z | 110 |
| P(K2≥K) | 0.10 | 0.05 | 0.01 | 0.005 |
| K | 2.706 | 3.841 | 6.635 | 7.879 |
(1)写出x,y,z的值
(2)根据以上列联表,问有多大把握认为“性别在购买食物时看营养说明”有关?
(3)从女生中按是否看营养说明采取分层抽样,抽取容量为5的样本,再从这5名女生中随机选取两名作深度访谈.求选到看与不看营养说明的女生各一名的概率.
分析 (1)利用列联表,可得x,y,z的值;
(2)根据性别与看营养说明列联表,求出K2的观测值k的值为7.486>6.635,再根据P(K2≥6.635)=0.01,该校高中学生“性别与在购买食物时看营养说明”有关.
(3)确定基本事件的个数,即可求选到看与不看营养说明的女生各一名的概率.
解答 解:(1)由题意,z=110-60=50,x=50-30=20,y=10+20=30;
(2)假设H0:该校高中学生性别与在购买食物时看营养说明无关,则K2应该很小.
根据题中的列联表得K2=$\frac{110×(50×20-30×10)^{2}}{80×30×60×50}$≈7.486>6.635,
由P(K2≥6.635)=0.01,
有99%的把握认为该校高中学生“性别与在购买食物时看营养说明”有关.
(3)从这5名女生中随机选取两名作深度访谈,共${C}_{5}^{2}$=10个基本事件,选到看的,有3人,与不看营养说明的,有2名,选到看与不看营养说明的女生各一名,共6个基本事件,
∴选到看与不看营养说明的女生各一名的概率为$\frac{6}{10}$=$\frac{3}{5}$.
点评 本题主要考查读图表、独立性检验等基础知识,考查数据处理能力和应用意识,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
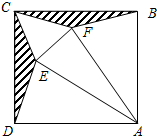 如图,将正方形剪去两个底角为15°的等腰三角形CDE和CBF,然后沿图中所画的线折成一个正三棱锥,这个正三棱锥侧面与底面所成的二面角的余弦值为$\frac{2\sqrt{3}}{3}-1$.
如图,将正方形剪去两个底角为15°的等腰三角形CDE和CBF,然后沿图中所画的线折成一个正三棱锥,这个正三棱锥侧面与底面所成的二面角的余弦值为$\frac{2\sqrt{3}}{3}-1$.