题目内容
2．下列说法正确的是（ ）①要得到函数y=lg（1-x）的图象，只需将函数y=lg（-x）的图象向左平移一个单位．
②要得到函数y=lg（1-x）的图象，只需将函数y=lg（-x）的图象向右平移一个单位．
③要得到函数y=lg（1-x）的图象，只需将函数y=lg（x+1）的图象关于y轴做对称．
④要得到函数y=lg（1-x）的图象，只需将函数y=lg（x-1）的图象关于y轴做对称．
| A． | ①③ | B． | ①④ | C． | ②③ | D． | ②④ |
分析 直接根据函数图象的变换规则考查各变换，其中y=lg[-（x-1）]，只需将y=lg（-x）图象向右平移一个单位即可得到；函数y=lg（1-x）的图象与函数y=lg（1+x）图象关于y轴对称．
解答 解：根据函数图象变换的规则逐个考察下列个变换：
①函数y=f（x）=lg（1-x）=lg[-（x-1）]，
因此只需将y=lg（-x）的图象向右平移一个单位即可得到f（x）的图象，所以①错误的；
②函数y=f（x）=lg（1-x）=lg[-（x-1）]，
因此只需将y=lg（-x）的图象向右平移一个单位即可得到f（x）的图象，所以②正确的；
③因为函数y=lg（1-x）的图象与函数y=lg（1+x）图象关于y轴对称，
所以，③是正确的；
④因为函数y=lg（1-x）的图象与函数y=lg（x-1）图象关于直线x=1轴对称，
所以，④是错误的；
故答案为：C．
点评 本题主要考查了函数的图象变换，涉及函数图象的平移变换和对称变换，掌握其变换规律时解题的关键，属于中档题．
练习册系列答案
相关题目
10．已知x，y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$，则z=2x-3y的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | 7 | D． | $-\frac{1}{2}$ |
11．函数$f（x）=-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+2x$的极大值点是（ ）
| A． | $-\frac{4}{5}$ | B． | 1 | C． | $\frac{7}{6}$ | D． | -2 |
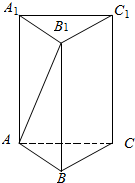如图，在正三棱柱ABC-A1B1C1中，若BB1=$\sqrt{2}$，AB=2$\sqrt{2}$，求点C到直线AB1的距离．