题目内容

4．已知集合A={x|3＜x＜6}，B={x|2＜x＜9}，
（I）求A∩B，（∁RA）∪（∁RB）
（II）已知C={x|a＜x＜2a-1}，若B∪C=B，求实数a的取值范围．

分析 （I）根据交集与并集、补集的定义，计算即可；
（II）由B∪C=B得C⊆B，讨论C=∅和C≠∅时，求出实数a的取值范围．

解答 解：（I）∵集合A={x|3＜x＜6}，B={x|2＜x＜9}，
∴A∩B={x|3＜x＜6}，
∴（∁RA）∪（∁RB）=∁R（A∩B）={x|x≤3或x≥6}；
（II）∵C={x|a＜x＜2a-1}，
且B∪C=B，∴C⊆B，
当C=∅时，a≥2a-1，解得a≤1；
当C≠∅时，解得2≤a≤5；
综上，实数a的取值范围是a≤1或2≤a≤5．

点评 本题考查了集合的定义与基本运算问题，是基础题．

练习册系列答案
相关题目
14．已知全集U={1，2，3，4，5，6，7}，集合A={1，3，7}，B={x|x=log2（a+1），a∈A}，则A∩B=（　　）
A．{1，3}B．{5，6}C．{4，5，6}D．{4，5，6，7}
15．设函数$f（x）=4sinx•{sin^2}（{\frac{π}{4}+\frac{x}{2}}）+cos2x$，若|f（x）-m|＜2成立的充分条件是$\frac{π}{6}≤x≤\frac{2π}{3}$，则实数m的取值范围为（0，5）．
12．设a为实数，函数f（x）=2x2+（x-a）•|x-a|．
（1）求f（x）的最小值；
（2）设h（x）=f（x）min，x∈（a，+∞），求不等式h（x）≥1的解集．
19．已知集合A={x|1＜x≤3}，B={x|x＜4，x∈Z}，则A∩B=（　　）
A．（2，3）B．[2，3]C．{2，3}D．{2，3，4}
9．已知e为自然对数的底数，若方程|xlnx-ex+e|=mx在区间[$\frac{1}{e}$，e2]上有三个不同实数根，则实数m的取值范围是[e-$\frac{1}{e}$-2，e-2）．
16．对于函数f（x）定义域中任意的x1，x2（x1≠x2），有如下结论：
①f（x1+x2）=f（x1）•f（x2）；
②f（x1•x2）=f（x1）•f（x2）；
③f（$\frac{{x}_{1}{+x}_{2}}{2}$）＞$\frac{f{（x}_{1}）+f{（x}_{2}）}{2}$；
④$\frac{f{（x}_{1}）-f{（x}_{2}）}{{x}_{1}{-x}_{2}}$＞0；
⑤当1＜x1＜x2时$\frac{f{（x}_{1}）}{{x}_{1}-1}＞\frac{f{（x}_{2}）}{{x}_{2}-1}$；
当f（x）=${（\frac{3}{2}）}^{x}$时，上述结论中正确结论的序号是①④⑤．
13．将函数f（x）=sin2x+$\sqrt{3}$cos2x图象上所有点向右平移$\frac{π}{6}$个单位长度，得到函数g （x）的图象，则g（x）图象的一个对称中心是（　　）
A．（$\frac{π}{3}$，0）B．（ $\frac{π}{4}$，0）C．（-$\frac{π}{12}$，0）D．（$\frac{π}{2}$，0）
14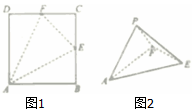．如图1，ABCD是边长为2的正方形，点E，F分别为BC，CD的中点，将△ABE，△ECF，△FDA分别沿AE，EF，FA折起，使B，C，D三点重合于点P，若四面体PAEF的四个顶点在同一个球面上，则该球的表面积是（　　）
A．$\sqrt{6}π$B．6πC．$4\sqrt{3}π$D．12π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网