题目内容
已知(
+
)n的第五项的二项式系数与第三项的二项式系数的比是14:3,
(1)求n.
(2)求展开式中常数项.
| x |
| 1 |
| 3x2 |
(1)求n.
(2)求展开式中常数项.
考点:二项式系数的性质
专题:二项式定理
分析:(1)由题意知
:
=14:3,由此求得n的值.
(2)在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
| C | 4 n |
| C | 2 n |
(2)在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
解答:
解:(1)由题意知
:
=14:3,即
=
=
,
化简可得 n2-5n-50=0,解得n=-5(舍去),或n=10.
(2)设该展开式中第r+1项中不含x,则 Tr+1=
•3-r•x
,
依题意,有x
=0,r=2.
所以,展开式中第三项为不含x的项,且T3=
•3-2=5.
| C | 4 n |
| C | 2 n |
| n(n-1)(n-2)(n-3) |
| 4! |
| n(n-1) |
| 2 |
| 14 |
| 3 |
化简可得 n2-5n-50=0,解得n=-5(舍去),或n=10.
(2)设该展开式中第r+1项中不含x,则 Tr+1=
| C | r 11 |
| 10-5r |
| 2 |
依题意,有x
| 10-5r |
| 2 |
所以,展开式中第三项为不含x的项,且T3=
| C | 2 10 |
点评:本题主要考查二项式系数的性质,二项展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合M={x|2x<
},N={x|-2≤x≤3},则M∩N=( )
| 1 |
| 2 |
| A、[-2,1) |
| B、[-2,-l) |
| C、(-1,3] |
| D、[-2,3] |
已知一几何体三视图如图,则其体积为( )
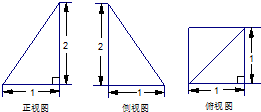

A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验如下:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验如下:
