题目内容
过点(-1,2)且与原点的距离最大的直线方程是( )
| A、x-2y+5=0 |
| B、x+2y-5=0 |
| C、x+3y-7=0 |
| D、3x+y-5=0 |
考点:点到直线的距离公式
专题:直线与圆
分析:可得当直线与点A(-1,2)且与原点O连线OA垂直时距离最大,进而可得直线的斜率,可得方程.
解答:
解:当直线与点A(-1,2)且与原点O连线OA垂直时距离最大,
由斜率公式可得kOA=
=-2,
∴所求直线的斜率为
,
故所求直线的方程为:y-2=
(x+1),
化为一般式可得:x-2y+5=0
故选:A.
由斜率公式可得kOA=
| 2-0 |
| -1-0 |
∴所求直线的斜率为
| 1 |
| 2 |
故所求直线的方程为:y-2=
| 1 |
| 2 |
化为一般式可得:x-2y+5=0
故选:A.
点评:本题考查点到直线的距离公式,涉及直线的一般式方程,属基础题.

练习册系列答案
相关题目
已知函数f(x)=
sin2x+cos2x,则( )
| 3 |
A、f(x)在(0,
| ||||
B、f(x)在(
| ||||
C、f(x)在(-
| ||||
D、f(x)在 (-
|
设复数ω1=-
+
i,ω2=cos
+isin
,若z=ω1•ω2,则复数z的虚部为( )
| 1 |
| 2 |
| ||
| 2 |
| π |
| 12 |
| π |
| 12 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
sin(-
)的值等于( )
| 5π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
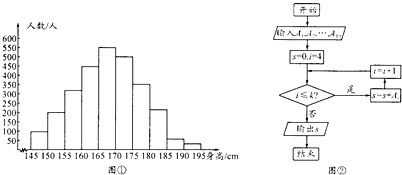
阅读如图所示的程序框图,运行相应的程序,输出的结果k=( )


| A、4 | B、5 | C、6 | D、7 |
已知
=(
,2sinα),
=(cosα,3),且
∥
.若α∈[0,2π],则α的值为( )
| a |
| 1 |
| 3 |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|