题目内容
18.直线y=$\sqrt{3}$x+1与直线$\sqrt{3}$x-3y+1=0的夹角是$\frac{π}{6}$.分析 由题意可得两直线的斜率,进而可得倾斜角,结合图象可得.
解答 解:∵直线y=$\sqrt{3}$x+1的斜率为k1=$\sqrt{3}$,
∴直线的倾斜角α=$\frac{π}{3}$,
又∵直线$\sqrt{3}$x-3y+1=0的斜率k2=$\frac{\sqrt{3}}{3}$,
∴直线的倾斜角β=$\frac{π}{6}$,
∴已知两直线的解集为$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题考查两直线的夹角与到角问题,求出直线的倾斜角是解决问题的关键,属基础题.

练习册系列答案
相关题目
9.设i为虚数单位,则复数$\frac{1-i}{i}$的共轭复数所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知i为虚数单位,若复数z满足|z-3-4i|=1,则|z|的最大值为( )
| A. | 4 | B. | 5 | C. | 4$\sqrt{2}$ | D. | 6 |
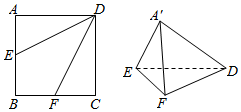 如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.
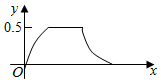
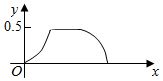
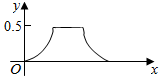
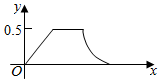
如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.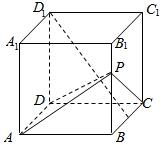 在边长为a的正方体ABCD-A1B1C1D1中,点P从B点开始按路径B→B1→C1→C运动,设从B点列P点的路程为x,V(x)表示空间几何体的体积,其中四校锥P-ABCD的体积为V1(x),剩余空间几何体的体积为V2(x).则f(x)=$\frac{{V}_{1}(x)}{{V}_{2}(x)}$的图象为( )
在边长为a的正方体ABCD-A1B1C1D1中,点P从B点开始按路径B→B1→C1→C运动,设从B点列P点的路程为x,V(x)表示空间几何体的体积,其中四校锥P-ABCD的体积为V1(x),剩余空间几何体的体积为V2(x).则f(x)=$\frac{{V}_{1}(x)}{{V}_{2}(x)}$的图象为( )