题目内容
定义在R上的奇函数f(x)的最小正周期为π.且当x∈[-
,0)时,f(x)=sinx,则f(-
)的值为 .
| π |
| 2 |
| 5π |
| 3 |
考点:函数奇偶性的性质
专题:函数的性质及应用,三角函数的求值
分析:本题可以利用函数的奇偶性和周期性,将自变量转化到区间[-
,0),再利用已知解析式求值,得到本题结论.
| π |
| 2 |
解答:
解:∵定义在R上的奇函数f(x)的最小正周期为π.
∴f(-x)=-f(x),f(x+kπ)=f(x),k∈Z.
∴f(-
)=f(-
+2π)=f(
)=-f(-
).
∵当x∈[-
,0)时,f(x)=sinx,
∴f(-
)=sin(-
)=-
.
∴f(-
)=
.
故答案为:
.
∴f(-x)=-f(x),f(x+kπ)=f(x),k∈Z.
∴f(-
| 5π |
| 3 |
| 5π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵当x∈[-
| π |
| 2 |
∴f(-
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
∴f(-
| 5π |
| 3 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了函数的奇偶性和周期性,还考查了三角函数求值的知识,本题难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
与向量
=(
-1,
+1)夹角角为
的单位向量是( )
| a |
| 3 |
| 3 |
| π |
| 4 |
A、(-
| ||||||||||||
B、(-
| ||||||||||||
C、(-
| ||||||||||||
D、(
|
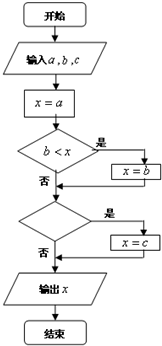 如图所示程序框图中,如果输入三个实数a、b、c,要求输出这三个数中最小的数,那么在空白的判断框中,应该填入下面四个选项中的( )
如图所示程序框图中,如果输入三个实数a、b、c,要求输出这三个数中最小的数,那么在空白的判断框中,应该填入下面四个选项中的( )| A、c<x | B、x<c |
| C、c<b | D、b<c |
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” |
| D、命题“若x=y,则cosx=cosy”的逆否命题为真命题 |
设随机变量X是离散型随机变量,X∽B(n,p)且EX=1.6,DX=1.28,则数对X~B(n,p)的取值为 ( )
| A、(8,0.2) |
| B、(5,0.32) |
| C、(7,0.45) |
| D、(4,0.4) |
 如图,PQ是半径为1的圆A的直径,△ABC是边长为1的正三角形,则
如图,PQ是半径为1的圆A的直径,△ABC是边长为1的正三角形,则| BP |
| CQ |
( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |