Question

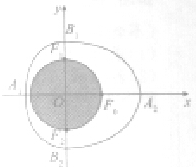某服饰公司设计类一款服饰饰品，如图外面是红色透明水晶材质，里面是一个球形绿色玉质宝珠，其轴截面呦半椭圆C₁：

x2

a2

+

y2

b2

=1，（x≥0）与半椭圆C₂：

y2

b2

+

x2

c2

=1，（x＜0），（其中a²=b²+c²，a＞b＞c＞0）组成．设点F₀、F₁、F₂是相应椭圆的焦点，A₁、A₂和B₁、B₂是轴截面与x，y轴的交点，阴影部分是宝珠轴截面，F₀、F₁、F₂在宝珠珠面上，则椭圆C₁的离心率为

 

．

Answer 1

考点：椭圆的应用

专题：圆锥曲线中的最值与范围问题

分析：仔细阅读题意得出得出圆的半径：r=

a2-b2

，r=

b2-c2

，结合a²=b²+c²，a＞b＞c＞0），求解a²=3c²，即求解得e=

3

3

．

解答： 解：设点F₀、F₁、F₂是相应椭圆的焦点，圆的图形，
∵其轴截面呦半椭圆C₁：

x2

a2

+

y2

b2

=1，（x≥0）与半椭圆C₂：

y2

b2

+

x2

c2

=1，（x＜0），（其中a²=b²+c²，a＞b＞c＞0）组成．
∴根据题意得出：r=

a2-b2

，r=

b2-c2

，
即：

a2-b2

=

b2-c2

，a²=2b²-c²，
∵a²=b²+c²，a＞b＞c＞0），
∴a²=2a²-2c²-c²，a²=3c²，

c2

a2

=

1

3

，e=

3

3

，
故答案为：

3

3

．

点评：本题考查了椭圆的方程，几何意义，圆等知识，结合实际问题求解，难度较大，关键是仔细阅读题目，找出等量关系即可．