题目内容
已知函数f（x）是偶函数，当x≥0时，f（x）=3x-9，则f（x-3）＞0的解集为 ．
考点：奇偶性与单调性的综合
专题：函数的性质及应用,不等式的解法及应用
分析：由当x≥0时，f（x）=3x-9，可得f（x）＞0时，x＞2；又由函数f（x）是偶函数，可得当x＜0，f（x）＞0时，x＜-2，进而得到f（x）＞0的解集，结合函数图象的平移变换，可得f（x-3）＞0的解集．
解答：
解：当x≥0时，f（x）=3x-9，
由f（x）＞0得：3x-9＞0，
解得：x＞2，
又∵函数f（x）是偶函数，
∴当x＜0时，解f（x）＞0得：x＜-2，
综上，f（x）＞0的解集为（-∞，-2）∪（2，+∞），
故f（x-3）＞0时，x-3∈（-∞，-2）∪（2，+∞），
即x∈（-∞，1）∪（5，+∞），
故答案为：（-∞，1）∪（5，+∞）
由f（x）＞0得：3x-9＞0，
解得：x＞2，
又∵函数f（x）是偶函数，
∴当x＜0时，解f（x）＞0得：x＜-2，
综上，f（x）＞0的解集为（-∞，-2）∪（2，+∞），
故f（x-3）＞0时，x-3∈（-∞，-2）∪（2，+∞），
即x∈（-∞，1）∪（5，+∞），
故答案为：（-∞，1）∪（5，+∞）
点评：本题考查的知识点是函数的奇偶性，函数图象的平移变换，指数不等式的解法，难度不大，属于基础题．
练习册系列答案
相关题目
函数f(x)=
的定义域是（ ）
| 1 | ||
|
| A、（-∞，9] |
| B、（-∞，9） |
| C、（0，9] |
| D、（0，9） |
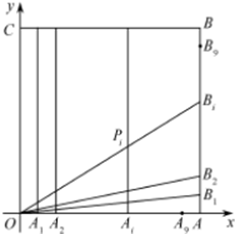如图，在正方形OABC中，O为坐标原点，点A的坐标为（10，0），点C的坐标为（0，10），分别将线段OA和AB十等分，分点分别记为A1，A2，…，A9和B1，B2，…，B9，连接OBi，过Ai作x轴的垂线与OBi，交于点Pi（i∈N*，1≤i≤9）．设非负实数x，y满足x-y+1≥0且3x+y-3≤0，则4x+y的最大值为（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、4 |
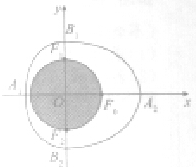某服饰公司设计类一款服饰饰品，如图外面是红色透明水晶材质，里面是一个球形绿色玉质宝珠，其轴截面呦半椭圆C1：