题目内容
函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),且关于x的不等式f(x)<c的解集为(m,m+6),在直线x=m,x=m+6,y=0,y=c围成的矩形内任意取一点P,则P点落在y=f(x)与y=c围成的封闭区域内的概率为 .
考点:定积分在求面积中的应用
专题:综合题,概率与统计
分析:根据函数的值域求出a与b的关系,然后根据不等式的解集可得f(x)=c的两个根为m,m+6,最后利用根与系数的关系建立等式,求出c,再以面积为测度,即可求出概率.
解答:
解:∵函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),
∴f(x)=x2+ax+b=0只有一个根,即△=a2-4b=0则b=
,
不等式f(x)<c的解集为(m,m+6),
即为x2+ax+
<c解集为(m,m+6),
则x2+ax+
-c=0的两个根为m,m+6
∴|m+6-m|=
=6
解得c=9.
对于抛物线f(x)=x2+ax+b(a,b∈R),不论a,b取何值,图形形状不变,所围成的面积为一定值,故令f(x)=x2,则
x2dx=18,y=f(x)与y=c围成的封闭区域的面积为36,
∵直线x=m,x=m+6,y=0,y=c围成的矩形的面积为54,
∴所求的概率为
=
.
故答案为:
.
∴f(x)=x2+ax+b=0只有一个根,即△=a2-4b=0则b=
| a2 |
| 4 |
不等式f(x)<c的解集为(m,m+6),
即为x2+ax+
| a2 |
| 4 |
则x2+ax+
| a2 |
| 4 |
∴|m+6-m|=
a2-4(
|
解得c=9.
对于抛物线f(x)=x2+ax+b(a,b∈R),不论a,b取何值,图形形状不变,所围成的面积为一定值,故令f(x)=x2,则
| ∫ | 3 -3 |
∵直线x=m,x=m+6,y=0,y=c围成的矩形的面积为54,
∴所求的概率为
| 36 |
| 54 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查了一元二次不等式的应用,以及根与系数的关系,考查几何概型,同时考查了分析求解的能力和计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
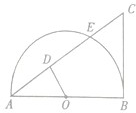 如图,过点C作半圆O的切线CB,切点为B,直线AC与半圆O的交点分别为A、E,过圆心O作OD⊥AC垂点为D.
如图,过点C作半圆O的切线CB,切点为B,直线AC与半圆O的交点分别为A、E,过圆心O作OD⊥AC垂点为D. 如图,圆O的半径为1,△ABC为圆O的内接正三角形,DA与圆O相切于点A,BD过圆心O且与圆相交于点E,则DE长为
如图,圆O的半径为1,△ABC为圆O的内接正三角形,DA与圆O相切于点A,BD过圆心O且与圆相交于点E,则DE长为