题目内容
如图:⊙O是ABC的内切圆,若∠DEF=55°,则∠BAC= .
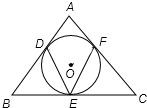

考点:与圆有关的比例线段
专题:选作题,立体几何
分析:连接OD、OF;根据切线的性质知:OD⊥AB,OF⊥AC,则四边形ADOF中,∠A+∠DOF=180°,那么解题的关键是求出∠DOF的度数,在⊙O中,∠DOF和∠DEF是同弧所对的圆心角和圆周角,根据圆周角定理,易求得∠DOF的度数,由此得解.
解答:
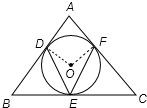 解:如图,连接OD、OE,则∠ODA=∠OFA=90°.
解:如图,连接OD、OE,则∠ODA=∠OFA=90°.
⊙O中,∠DOF=2∠DEF=2×55°=110°.
四边形ADEF中,∠ODA=∠OFA=90°,
∴∠BAC+∠DOF=180°,
即∠BAC=180°-∠DOF=70°.
故答案为:70°.
 解:如图,连接OD、OE,则∠ODA=∠OFA=90°.
解:如图,连接OD、OE,则∠ODA=∠OFA=90°.⊙O中,∠DOF=2∠DEF=2×55°=110°.
四边形ADEF中,∠ODA=∠OFA=90°,
∴∠BAC+∠DOF=180°,
即∠BAC=180°-∠DOF=70°.
故答案为:70°.
点评:本题考查的是圆的切线的性质定理的证明、圆周角定理以及三角形内切圆的性质.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
下列命题错误的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1” |
| B、若命题p:?x0∈R,x02-x0+1≤0,则¬p:?x∈R,x2-x+1>0 |
| C、△ABC中,sinA>sinB是A>B的充要条件 |
| D、若p∨q为真命题,则p、q均为真命题 |
 如图,直四棱柱ABCD-A1B1C1D1的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,P、是CC1的中点,求证:PB∥面AD1C.(用两种方法)
如图,直四棱柱ABCD-A1B1C1D1的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,P、是CC1的中点,求证:PB∥面AD1C.(用两种方法)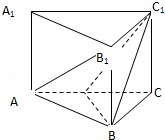 已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.
已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.