题目内容
14．某公司门前有一排9个车位的停车场，从左往右数第三个，第七个车位分别停着A车和B车，同时进来C，D两车，在C，D不相邻的条件下，C和D至少有一辆与A和B车相邻的概率是（ ）| A． | $\frac{10}{17}$ | B． | $\frac{14}{17}$ | C． | $\frac{9}{16}$ | D． | $\frac{7}{9}$ |
分析 先求出基本事件总数n=${A}_{7}^{2}-{A}_{2}^{2}-{A}_{2}^{2}{A}_{2}^{2}-{A}_{2}^{2}$=34，C和D至少有一辆与A和B车相邻的对立事件是C和D都不与A和B车相邻，由此能求出C和D至少有一辆与A和B车相邻的概率．
解答 解：某公司门前有一排9个车位的停车场，从左往右数第三个，第七个车位分别停着A车和B车，
同时进来C，D两车，在C，D不相邻的条件下，
基本事件总数n=${A}_{7}^{2}-{A}_{2}^{2}-{A}_{2}^{2}{A}_{2}^{2}-{A}_{2}^{2}$=34，
C和D至少有一辆与A和B车相邻的对立事件是C和D都不与A和B车相邻，
∴C和D至少有一辆与A和B车相邻的概率：
p=1-$\frac{{A}_{3}^{2}}{34}$=$\frac{14}{17}$．
故选：B．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．
练习册系列答案
相关题目
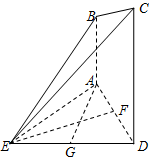如图，在平面ABCD中，AB⊥平面ADE，CD⊥平面ADE，△ADE是等边三角形，AD=DC=2AB=2，F，G分别为AD，DE的中点．
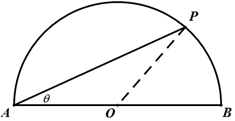运动员小王在一个如图所示的半圆形水域（O为圆心，AB是半圆的直径）进行体育训练，小王先从点A出发，沿着线段AP游泳至半圆上某点P处，再从点P沿着弧PB跑步至点B处，最后沿着线段BA骑自行车回到点A处，本次训练结束．已知OA=1500m，小王游泳、跑步、骑自行车的平均速度分别为2m/s，4m/s，10m/s，设∠PAO=θrad．
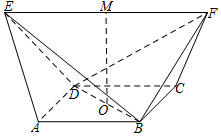如图，在五面体ABCDEF中，底面ABCD是正方形，△ADE，△BCF都是等边三角形，EF∥AB，且EF＞AB，M，O分别为EF，BD的中点，连接MO．
6．《算数书》竹简于上世纪八十年代在湖北省张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“禾盖”的术：置如其周，令相乘也．又以高乘之，三十六成一．该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式V≈$\frac{1}{36}$L2h．它实际上是将圆锥体积公式中的圆周率π近似取为3．那么，近似公式V≈$\frac{7}{264}$L2h相当于将圆锥体积公式中的圆周率π近似取为（ ）
| A． | $\frac{22}{7}$ | B． | $\frac{25}{8}$ | C． | $\frac{23}{7}$ | D． | $\frac{157}{50}$ |
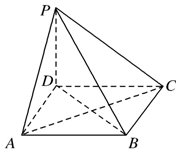如图，在四棱锥 P-ABCD中，底面是边长为a的正方形，侧棱PD=a，PA=PC=$\sqrt{2}$a．