题目内容
已知函数f（x）=
在R上单调递减，则a的取值范围是 ．
|
考点：函数单调性的性质
专题：函数的性质及应用
分析：由题意根据函数的单调性的性质可得
，由此求得a的范围．
|
解答：
解：由于函数f（x）=
在R上单调递减，故有
，
求得
＜a≤
，
故答案为：（
，
]．
|
|
求得
| 1 |
| 6 |
| 1 |
| 5 |
故答案为：（
| 1 |
| 6 |
| 1 |
| 5 |
点评：本题主要考查函数的单调性的性质，属于基础题．
练习册系列答案
相关题目
设全集为R，函数f（x）=ln
的定义域为M，则∁RM为（ ）
| 1+x |
| 1-x |
| A、（-1，1） |
| B、（-∞，-1）∪（1，+∞） |
| C、（-∞，-1]∪[1，+∞） |
| D、[-1，1] |
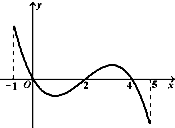已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．下列关于f（x）的命题：