题目内容
已知函数 ;
;
(I)若 >0,试判断f(x)在定义域内的单调性;
>0,试判断f(x)在定义域内的单调性;
(II)若f(x)在[1,e]上的最小值为 ,求
,求 的值;
的值;
(III)若f(x)<x2在(1, 上恒成立,求a的取值范围.
上恒成立,求a的取值范围.
.解:(I)由题意f(x)的定义域为(0,+∞),且f'(x)= …
…
∵a>0,
∴f'(x)>0,
故f(x)在(0,+∞)上是单调递增函数
(II)由(I)可知,f′(x)= .
.
(1)若a≥﹣1,则x+a≥0,即f′(x)≥0在[1,e]上恒成立,此时f(x)在[1,e]上为增函数,
∴[f(x)]min=f(1)=﹣a= ,
,
∴a=﹣ (舍去)
(舍去)
(2)若a≤﹣e,则x+a≤0,即f′(x)≤0在[1,e]上恒成立,此时f(x)在[1,e]上为减函数,
∴[f(x)]min=f(e)=1﹣ (舍去)
(舍去)
(3)若﹣e<a<﹣1,令f'(x)=0得x=﹣a,当1<x<﹣a时,f'(x)<0,
∴f(x)在(1,﹣a)上为减函数,f(x)在(﹣a,e)上为增函数,
∴[f(x)]min=f(﹣a)=ln(﹣a)+1=
∴[f(x)]min=f(﹣a)=ln(﹣a)+1=
∴a=﹣ .
.


练习册系列答案
相关题目
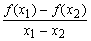 >0,则下列命题中正确的有 。
>0,则下列命题中正确的有 。 是减函数的概率为 。
是减函数的概率为 。 的导数为
的导数为 ,则数列
,则数列 的前
的前 项和是( )
项和是( ) B.
B. C.
C. D.
D.
 ;
; 求
求 的值;
的值; 求实数
求实数 的值.
的值. 在R上可导,且
在R上可导,且 =
= ,则( )
,则( ) B.
B.  C.
C. D. 不能确定
D. 不能确定 在x=1处取极值,则a=________.
在x=1处取极值,则a=________. (其中
(其中 )的部分图像如下图所示,则
)的部分图像如下图所示,则 的值为( )
的值为( ) B.
B. C.
C.  D.
D.

 有极值,则导函数
有极值,则导函数 的图象不可能是 ( )
的图象不可能是 ( )