题目内容
已知函数f(x)=2x+k•2-x(k∈R).
(1)若函数f(x)为奇函数,求k的值;
(2)若函数f(x)在(-∞,2]上为减函数,求k的取值范围.
(1)若函数f(x)为奇函数,求k的值;
(2)若函数f(x)在(-∞,2]上为减函数,求k的取值范围.
考点:函数奇偶性的性质,函数单调性的性质
专题:函数的性质及应用
分析:(1)根据奇函数的概念,f(x)+f(-x)=0,解答即可;
(2)先讨论K的取值范围,再求取值范围
(2)先讨论K的取值范围,再求取值范围
解答:
解:(1)f(x)+f(-x)=(k+1)(2x+2-x)=0对一切的x∈R成立,
所以k=-1.
(2)若k≤0,则函数f(x)在(-∞,2]单调递增(舍),
当k>0时,令t=2x∈(0,4],
则函数g(t)=t+
在(0,4]上单调递减,
所以
≥4,
即k≥16.
所以k=-1.
(2)若k≤0,则函数f(x)在(-∞,2]单调递增(舍),
当k>0时,令t=2x∈(0,4],
则函数g(t)=t+
| k |
| t |
所以
| k |
即k≥16.
点评:本题主要考查奇函数的性质,单调性的定义.

练习册系列答案
相关题目
某程序框图如图所示,执行该程序后输出的S的值是( )
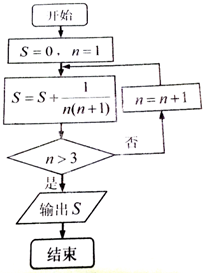

A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={3,5,6,8},B={1,3,5},那么A∪B等于( )
| A、{1,3,5,6,8} |
| B、{6,8} |
| C、{3,5} |
| D、{1,6,8} |
 如图,正四棱锥S-ABCD,底面边长与高都是2,K是SC的中点,T是SB的中点.
如图,正四棱锥S-ABCD,底面边长与高都是2,K是SC的中点,T是SB的中点.