题目内容
已知圆C1:x2+y2-6x-7=0与圆C2:x2+y2-6y-27=0相交于A、B两点,则线段AB的中垂线方程为 .
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:由题意可知所求线段AB的中垂线方程就是两个圆的圆心连线方程,求出两个圆的圆心坐标,二行求解直线方程.
解答:
解:圆C1:x2+y2-6x-7=0圆心坐标(3,0)与圆C2:x2+y2-6y-27=0的圆心坐标(0,3),
圆C1:x2+y2-6x-7=0与圆C2:x2+y2-6y-27=0相交于A、B两点,
线段AB的中垂线方程就是两个圆的圆心连线方程,
在AB的斜率为:-1,所求直线方程为:y=-(x-3).
即x+y-3=0.
故答案为:x+y-3=0.
圆C1:x2+y2-6x-7=0与圆C2:x2+y2-6y-27=0相交于A、B两点,
线段AB的中垂线方程就是两个圆的圆心连线方程,
在AB的斜率为:-1,所求直线方程为:y=-(x-3).
即x+y-3=0.
故答案为:x+y-3=0.
点评:本题考查两个圆的位置关系的应用,正确判断所求直线方程与圆的位置关系是解题的关键.

练习册系列答案
相关题目
已知函数f(x)的图象如图所示,则它的一个可能的解析式为( )
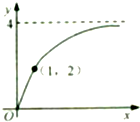

A、y=2
| ||
B、y=2x
| ||
| C、y=log2(x+3) | ||
D、y=4-
|
下列命题错误的是( )
| A、命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1≥0” | ||||||||
| B、若p∧q为假命题,则p,q均为假命题 | ||||||||
C、若a,b∈[0,1],则不等式a2+b2<
| ||||||||
D、“平面向量
|
若f(x)=
,则f(3)=( )
| x+1 |
| A、2 | ||
| B、2或-2 | ||
C、2
| ||
| D、-2 |