题目内容
20.双曲线C1:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦点为F1,F2,其中F2为抛物线C2:y2=2px(p>0)的焦点,设C1与C2的一个交点为P,若|PF2|=|F1F2|,则C1的离心率为$\sqrt{2}$+1.分析 设P(m,n)位于第一象限,求出抛物线的焦点和准线方程,可得c=$\frac{p}{2}$,再由抛物线的定义,求得m,代入抛物线的方程可得n,代入双曲线的方程,由双曲线的a,b,c和离心率公式,化简整理计算即可得到所求值.
解答 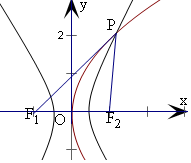 解:设P(m,n)位于第一象限,可得m>0,n>0,
解:设P(m,n)位于第一象限,可得m>0,n>0,
由题意可得F2($\frac{p}{2}$,0),且双曲线的c=$\frac{p}{2}$,
抛物线的焦点为准线方程为x=-$\frac{p}{2}$,
由抛物线的定义可得m+$\frac{p}{2}$=|PF2|=|F1F2|=2c,
即有m=c,n=$\sqrt{2pm}$=$\sqrt{4{c}^{2}}$=2c,
即P(c,2c),代入双曲线的方程可得,
$\frac{{c}^{2}}{{a}^{2}}$-$\frac{4{c}^{2}}{{b}^{2}}$=1,
即为e2-$\frac{4{e}^{2}}{{e}^{2}-1}$=1,
化为e4-6e2+1=0,
解得e2=3+2$\sqrt{2}$(3-2$\sqrt{2}$舍去),
可得e=1+$\sqrt{2}$.
故答案为:1+$\sqrt{2}$.
点评 本题考查双曲线的离心率的求法,注意运用抛物线的定义和点满足双曲线的方程,考查化简整理的运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.若f(x)=2xf'(1)+x2,则f'(0)=( )
| A. | $\frac{1}{2}$ | B. | 6 | C. | -2 | D. | -4 |
11.已知数列{an}为等差数列,若a8=4,则数列{an}的前15项和S15=( )
| A. | 12 | B. | 32 | C. | 60 | D. | 120 |
8. 已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )
已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )
 已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )
已知全集U=R,集合A={x|x2-2x≤0},B={y|y=sinx,x∈R},则图中阴影部分表示的集合为( )| A. | [-1,2] | B. | [-1,0)∪(1,2] | C. | [0,1] | D. | (-∞,-1)∪(2,+∞) |
12.在△ABC中,AC=$\sqrt{2}$,AB=2,∠BAC=135°,D是BC的中点,M是AD上一点,且$\overrightarrow{AM}$=2$\overrightarrow{MD}$,则$\overrightarrow{MB}$•$\overrightarrow{MC}$的值是( )
| A. | -$\frac{22}{9}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{7}{3}$ | D. | -$\frac{5}{3}$ |
9.在平面直角坐标系xOy中,圆O的方程为x2+y2=4,直线l的方程为y=k(x+2),若在圆O上至少存在三点到直线l的距离为1,则实数k的取值范围是( )
| A. | $[{0,\frac{{\sqrt{3}}}{3}}]$ | B. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | C. | $[{-\frac{1}{2},\frac{1}{2}}]$ | D. | $[{0,\frac{1}{2}}]$ |
10.已知函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的最小正周期为π,将该函数的图象向左平移$\frac{π}{6}$个单位后,得到的图象对应的函数为奇函数,则f(x)的图象( )
| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于直线x=$\frac{5π}{12}$对称 | ||
| C. | 关于点($\frac{5π}{12}$,0)对称 | D. | 关于直线x=$\frac{π}{12}$对称 |