题目内容
9.在平面直角坐标系xOy中,圆O的方程为x2+y2=4,直线l的方程为y=k(x+2),若在圆O上至少存在三点到直线l的距离为1,则实数k的取值范围是( )| A. | $[{0,\frac{{\sqrt{3}}}{3}}]$ | B. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | C. | $[{-\frac{1}{2},\frac{1}{2}}]$ | D. | $[{0,\frac{1}{2}}]$ |
分析 求出圆心O(0,0),半径r=2,由在圆O上至少存在三点到直线l的距离为1,得到圆心O(0,0)到直线y=k(x+2)的距离d≤1,由此能求出实数k的取值范围.
解答 解:∵圆O的方程为x2+y2=4,直线l的方程为y=k(x+2),
∴圆心O(0,0),半径r=2,
∵在圆O上至少存在三点到直线l的距离为1,
∴圆心O(0,0)到直线y=k(x+2)的距离d≤1,
即d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$≤1,
解得-$\frac{\sqrt{3}}{3}≤k≤\frac{\sqrt{3}}{3}$.
∴实数k的取值范围是[-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$].
故选:B.
点评 本题考查实数的取值范围的求法,考查圆、直线方程、点到直线距离公式等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.复数$z=\frac{{({1-i})({4-i})}}{1+i}$的共轭复数是( )
| A. | -4i | B. | -4 | C. | 4i | D. | -1+4i |
14.设集合A={x|x<2},B={y|y=2x-1},则A∩B=( )
| A. | (-∞,3) | B. | [2,3) | C. | (-∞,2) | D. | (-1,2) |
1.设集合A={x|x<2},B={y|y=2x-1},则A∩B=( )
| A. | [-1,2) | B. | (0,2) | C. | (-∞,2) | D. | (-1,2) |
 ,
,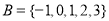 ,则
,则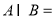 ( )
( )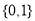 B.
B.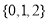 C.
C.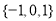 D.
D.