题目内容
10.已知函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的最小正周期为π,将该函数的图象向左平移$\frac{π}{6}$个单位后,得到的图象对应的函数为奇函数,则f(x)的图象( )| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于直线x=$\frac{5π}{12}$对称 | ||
| C. | 关于点($\frac{5π}{12}$,0)对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
分析 根据函数f(x的最小正周期为π,求出ω,向左平移$\frac{π}{6}$个单位后,得到的图象对应的函数为奇函数,求出φ.可得f(x)的解析式.结合三角函数的性质可得对称中心和对称轴.
解答 解:函数f(x)=sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的最小正周期为π,
∴$π=\frac{2π}{ω}$,
∴ω=2.
∴f(x)=sin(2x+φ),
将f(x)图象向左平移$\frac{π}{6}$个单位后,可得sin(2x$+\frac{π}{3}$+φ),函数为奇函数,
∴$\frac{π}{3}$+φ=kπ,
∵-$\frac{π}{2}$<φ<$\frac{π}{2}$,
∴φ=$-\frac{π}{3}$,
∴f(x)=sin(2x$-\frac{π}{3}$),
令2x$-\frac{π}{3}$=kπ,
可得x=$\frac{1}{2}$kπ$+\frac{π}{6}$,k∈Z.
考查A,C选项不对.
令2x$-\frac{π}{3}$=kπ$+\frac{π}{2}$,
可得x=$\frac{1}{2}$kπ+$\frac{5π}{12}$,k∈Z.
考查B选项对.
故选B.
点评 本题给出正弦型三角函数的图象即现在,确定其解析式实关键,属于基础题.

练习册系列答案
相关题目
1.设集合A={x|x<2},B={y|y=2x-1},则A∩B=( )
| A. | [-1,2) | B. | (0,2) | C. | (-∞,2) | D. | (-1,2) |
5.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线与直线x=$\frac{{a}^{2}}{c}$分别交于A,B两点,F为该双曲线的右焦点,若90°<∠AFB<120°,则该双曲线离心率的取值范围是( )
| A. | (1,$\sqrt{2}$) | B. | ($\frac{2\sqrt{3}}{3}$,+∞) | C. | (1,$\frac{2\sqrt{3}}{3}$) | D. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$) |
 ,全集U=R。
,全集U=R。 时,求
时,求 和
和 ;
; ,求实数
,求实数 的取范围。
的取范围。 ,
,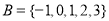 ,则
,则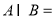 ( )
( )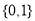 B.
B.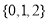 C.
C.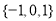 D.
D.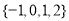
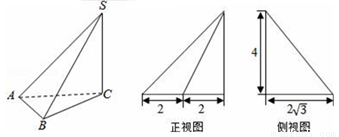
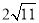 B.
B.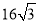 C.
C.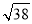 D.
D.