题目内容
椭圆3x2+ky2=1的一个焦点的坐标为（0，1），则其离心率为（ ）
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据题意可知a和b，进而根据c2=
-
=1求得k，即可求得e．
| 1 |
| k |
| 1 |
| 3 |
解答：
解：由题意，b2=
，a2=
∴c2=
-
=1，
∴k=
∴e2=k=
∴e=
故选D．
| 1 |
| 3 |
| 1 |
| k |
∴c2=
| 1 |
| k |
| 1 |
| 3 |
∴k=
| 3 |
| 4 |
∴e2=k=
| 3 |
| 4 |
∴e=
| ||
| 2 |
故选D．
点评：本题主要考查椭圆的性质，考查学生的计算能力．属基础题．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
在半径为5的圆中，圆心角为周长的
的角所对圆弧的长是（ ）
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列四个命题中，为真命题的是（ ）
| A、若a＞b，则ac2＞bc2 | ||||
| B、若a＞b，c＞d则a-c＞b-d | ||||
| C、若a＞|b|，则a2＞b2 | ||||
D、若a＞b，则
|
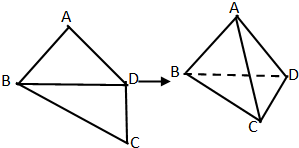如图所示，平面四边形ABCD中，AB=AD=CD=1，BD=| 2 |
BD⊥CD，将其沿对角线BD折成四面体A-BCD，使平面ABD⊥平面BCD，则下列说法中不正确的是（ ）
| A、平面ACD⊥平面ABD |
| B、AB⊥CD |
| C、平面ABC⊥平面ACD |
| D、AD⊥平面ABC |