题目内容
 如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,且DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,且DM=2| 2 |
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求点B到平面DOM的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定,平面与平面垂直的判定
专题:计算题,空间位置关系与距离
分析:(1)根据三角形的中位线定理,可得OM∥AB.再由线面平行判定定理,得到OM∥平面ABD;
(2)在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4,OD=
BD=2,从而算出∠DOM=90°,即OD⊥OM.根据OD⊥AC,利用线面垂直判定定理得到OD⊥平面ABC,进而得出平面DOM⊥平面ABC.
(3)分别算出△DOM的△ABC面积,利用三棱锥B-DOM与三棱锥D-BOM体积相等加以计算,可得点B到平面DOM的距离.
(2)在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4,OD=
| 1 |
| 2 |
(3)分别算出△DOM的△ABC面积,利用三棱锥B-DOM与三棱锥D-BOM体积相等加以计算,可得点B到平面DOM的距离.
解答:
解:(1)∵△ABC中,O为AC的中点,M为BC的中点,
∴OM∥AB.
∵OM?平面ABD,AB?平面ABD,
∴OM∥平面ABD.
(2)∵在菱形ABCD中,OD⊥AC,
∴在三棱锥B-ACD中,OD⊥AC.
在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4.
∵O为BD的中点,∴OD=
BD=2.
∵O为AC的中点,M为BC的中点,∴OM=
AB=2
又∵OD2+OM2=8=DM2,∴∠DOM=90°,即OD⊥OM.
∵AC?平面ABC,OM?平面ABC,AC∩OM=O,
∴OD⊥平面ABC.
∵OD?平面DOM,∴平面DOM⊥平面ABC.
(3)由(2)得OD⊥平面BOM,可得OD是三棱锥D-BOM的高.
设点B到面DOM距离为h,由OD=2,
∴S△ABC=
×OB×BMsin60°=
,S△DOM=
×OD×OM=2
∵因为VB-DOM=VD-BOM,
∴
S△DOM•h=
S△ABC•OD,即
×2h=
×
×2,解得h=
,
即点B到平面DOM的距离等于
.
∴OM∥AB.
∵OM?平面ABD,AB?平面ABD,
∴OM∥平面ABD.
(2)∵在菱形ABCD中,OD⊥AC,
∴在三棱锥B-ACD中,OD⊥AC.
在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4.
∵O为BD的中点,∴OD=
| 1 |
| 2 |
∵O为AC的中点,M为BC的中点,∴OM=
| 1 |
| 2 |
又∵OD2+OM2=8=DM2,∴∠DOM=90°,即OD⊥OM.
∵AC?平面ABC,OM?平面ABC,AC∩OM=O,
∴OD⊥平面ABC.
∵OD?平面DOM,∴平面DOM⊥平面ABC.
(3)由(2)得OD⊥平面BOM,可得OD是三棱锥D-BOM的高.
设点B到面DOM距离为h,由OD=2,
∴S△ABC=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
∵因为VB-DOM=VD-BOM,
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
即点B到平面DOM的距离等于
| 3 |
点评:本题给出平面图形的翻折,求证线面平行、面面垂直,并求点到平面的距离.着重考查了线面平行判定定理、面面垂直与线面性质和性质、利用等体积法求点面距离等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果执行如图的框图,输入N=5,则输出的数等于( )


A、
| ||
B、
| ||
C、
| ||
D、
|
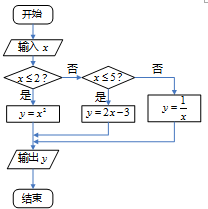 给出了一个程序框图,其作用是输入x的值,输出相应的y的值,
给出了一个程序框图,其作用是输入x的值,输出相应的y的值, 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2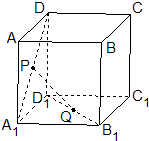 正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.
正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.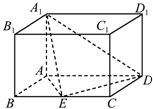 如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=
如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=