题目内容
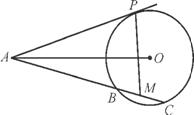
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过点C.已知AB=3 m,AD=2 m.
(1) 要使矩形AMPN的面积大于32 m2,则AN的长应在什么范围内?
(2) 当AN的长度是多少时,矩形AMPN的面积最小?并求最小面积.
(3) 若AN的长度不少于6 m,则当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
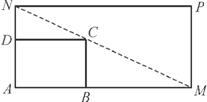
(1) 设AN=x m(x>2),则ND=x-2.
因为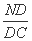 =
=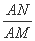 ,即
,即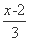 =
=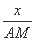 ,所以AM=
,所以AM=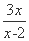 .
.
因为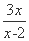 ·x>32,所以3x2-32x+64>0,即(3x-8)(x-8)>0,
·x>32,所以3x2-32x+64>0,即(3x-8)(x-8)>0,
所以2<x<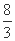 或x>8.
或x>8.
即满足题意的AN的取值范围为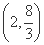 ∪(8,+∞).
∪(8,+∞).
(2) S矩形AMPN=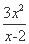
=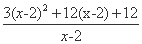
=3(x-2)+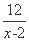 +12
+12
≥2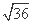 +12=24,
+12=24,
当且仅当x=4时取等号,即当AN=4m时,矩形AMPN的面积最小,最小面积为24 m2.
(3) 因为S矩形AMPN=3(x-2)+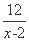 +12(x≥6),
+12(x≥6),
令x-2=t(t≥4),则f(t)=3t+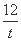 +12.
+12.
因为f'(t)=3-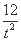 ,当t≥4时,f'(t)>0,
,当t≥4时,f'(t)>0,
所以f(t)=3t+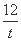 +12在[4,+∞)上单调递增,
+12在[4,+∞)上单调递增,
所以f(t)min=f(4)=27,此时x=6.
故当AN的长度是6 m时,矩形AMPN的面积最小,最小面积为27 m2.

练习册系列答案
相关题目
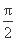 .
.
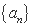 ,
,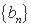 满足an+1=3an+2bn,bn+1=2bn,且满足
满足an+1=3an+2bn,bn+1=2bn,且满足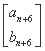 =M
=M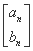 ,求二阶矩阵M.
,求二阶矩阵M.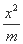 +
+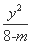 =1.
=1.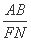 是定值;并求出这个定值.
是定值;并求出这个定值.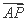 =
=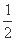 sin2θ·
sin2θ·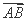 +cos2θ·
+cos2θ·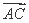 (θ∈R),则(
(θ∈R),则(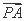 +
+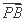 )·
)·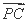 的最小值是 .
的最小值是 . 