题目内容
求证:n3+5n(n∈N*)能被6整除.
(1) 当n=1时,n3+5n=6能被6整除.
(2) 假设当n=k(k≥1,且k∈N*)时,k3+5k能被6整除;
则当n=k+1时,
(k+1)3+5(k+1)=k3+3k2+3k+1+5k+5=k3+5k+3k(k+1)+6.
由假设知k3+5k能被6整除,而3k(k+1),6也能被6整除,
所以(k+1)3+5(k+1)能被6整除.
由(1)(2)可知, 命题对任意n∈N*都成立.
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过点A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:
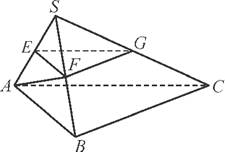
A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且AB=BC=CA=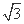
,AD=CD=1.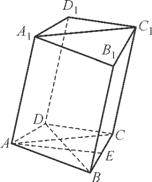
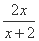,x1=1,xn=f(
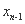)(n≥2,n∈N+).
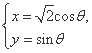(θ为参数),过点P(2,1)的直线与曲线C交于A,B两点.若PA·PB=
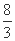,求AB的值.