题目内容
1.已知函数f(x)=xlnx-mx的图象与直线y=-1相切.(Ⅰ)求m的值,并求f(x)的单调区间;
(Ⅱ)若g(x)=ax3,设h(x)=f(x)-g(x),讨论函数h(x)的零点个数.
分析 (Ⅰ)确定函数的定义域,利用导数的几何意义,从而可求m的值和函数的单调区间;
(Ⅱ)构造函数,利用导数,求出函数的最值,再分类讨论即可得到函数零点的个数
解答 解:( I)设f(x)的图象与直线y=-1相切于点(x0,-1),(x0>0),
f′(x)=lnx+1-m,(x>0)
则$\left\{{\begin{array}{l}{{f^'}({x_0})=0}\\{f({x_0})=-1}\end{array}}\right.$即$\left\{{\begin{array}{l}{ln{x_0}+1-m=0}\\{{x_0}ln{x_0}-m{x_0}=-1}\end{array}}\right.$
解得:x0=1,m=1,
由f′(x)=lnx>0得x>1;f′(x)=lnx<0得0<x<1;
所以函数f(x)的单调减区间为(0,1);增区间为(1,+∞),
( II)h(x)=f(x)-g(x)=xlnx-x-ax3=x(lnx-1-ax2)(x>0).
由h(x)=0得$lnx-1-a{x^2}=0即a=\frac{lnx-1}{x^2}$;
∴$函数h(x)的零点个数即为函数y=a与y=\frac{lnx-1}{x^2}的图象的交点个数$.
记函数$r(x)=\frac{lnx-1}{x^2}$,
${r^'}(x)=\frac{x-2x(lnx-1)}{x^4}=\frac{3-2lnx}{x^3}$
由r′(x)>0得$0<x<{e^{\frac{3}{2}}}$;r′(x)<0得$x>{e^{\frac{3}{2}}}$,
∴r(x)在$(0,{e^{\frac{3}{2}}})$上单调递增;在$({e^{\frac{3}{2}}},+∞)$上单调递减,
∴$r{(x)_{max}}=r({e^{\frac{3}{2}}})=\frac{1}{{2{e^3}}}$,
又$x∈({e^{\frac{3}{2}}},+∞)$时,r(x)>0;x∈(0,e)时,r(x)<0;且x趋向于0时r(x)趋向于负无穷大.
∴当a>$\frac{1}{2{e}^{3}}$时,y=a与y=r(x)的图象无交点,函数h(x)无零点;
当a≤0或a=$\frac{1}{2{e}^{3}}$时,y=a与y=r(x)的图象恰有一个交点,函数h(x)恰有一个零点;
当0<a<$\frac{1}{2{e}^{3}}$时,y=a与y=r(x)的图象恰有两个交点,函数h(x)恰有两个个零点.
点评 本题考查了导数与函数的单调性的关系,函数最值的求法,函数零点个数的判断,属于中档题.

| A. | ?x0∈R,使得x02-x0+2=0 | |
| B. | 命题“?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 在△ABC中,“A=B”是“sinA=sinB”的充要条件 |
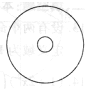 如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{21}{25}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |

| A. | $\frac{1}{55}$ | B. | $\frac{1}{58}$ | C. | $\frac{1}{61}$ | D. | $\frac{1}{64}$ |
| A. | -1 | B. | -i | C. | $\sqrt{2}i$ | D. | $-\sqrt{2}$ |
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
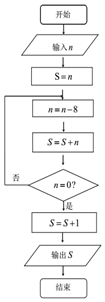 《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.
《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.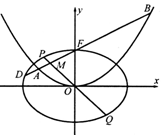 如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.
如图,在平面直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,抛物线C2:x2=4y的焦点F是C1的一个顶点.