题目内容
 如图,四边形ABCD中,AB=AD=CD=1,BD=
如图,四边形ABCD中,AB=AD=CD=1,BD=| 2 |
| A、A′C⊥BD | ||
| B、∠BA′C=90° | ||
| C、CA′与平面A′BD所成的角为30° | ||
D、四面体A′-BCD的体积为
|
考点:平面与平面垂直的性质
专题:计算题,空间位置关系与距离
分析:根据题意,依次分析命题:对于A可利用反证法说明真假;对于B△BA'D为等腰Rt△,CD⊥平面A'BD,得BA'⊥平面A'CD,根据线面垂直可知∠BA′C=90°;对于C由CA'与平面A'BD所成的角为∠CA'D=45°知C的真假;,对于D利用等体积法求出所求体积进行判定即可,综合可得答案.
解答:
解:若A成立可得BD⊥A'D,产生矛盾,故A不正确;
由题设知:△BA'D为等腰Rt△,CD⊥平面A'BD,得BA'⊥平面A'CD,于是B正确;
由CA'与平面A'BD所成的角为∠CA'D=45°知C不正确;
VA′-BCD=VC-A′BD=
,D不正确.
故选B.
由题设知:△BA'D为等腰Rt△,CD⊥平面A'BD,得BA'⊥平面A'CD,于是B正确;
由CA'与平面A'BD所成的角为∠CA'D=45°知C不正确;
VA′-BCD=VC-A′BD=
| 1 |
| 6 |
故选B.
点评:本题主要考查了异面直线及其所成的角,以及三棱锥的体积的计算,同时考查了空间想象能力,论证推理能力,解题的关键是须对每一个进行逐一判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
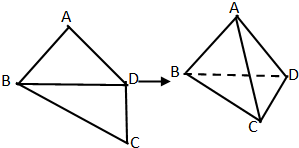 如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=
如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=| 2 |
BD⊥CD,将其沿对角线BD折成四面体A-BCD,使平面ABD⊥平面BCD,则下列说法中不正确的是( )
| A、平面ACD⊥平面ABD |
| B、AB⊥CD |
| C、平面ABC⊥平面ACD |
| D、AD⊥平面ABC |
已知函数f(x)=x3+x2+x+1,则f(x)在(0,1)处的切线方程为( )
| A、x-y-1=0 |
| B、x+y+1=0 |
| C、x-y+1=0 |
| D、x+y-1=0 |
下列几个图形中,可以表示函数关系f(x)的一个图是( )
A、 |
B、 |
C、 |
D、 |
“x≠2或y≠-2”是“xy≠-4”的( )
| A、必要而不充分条件 |
| B、充分而不要条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |