题目内容
11.$\int{\begin{array}{l}{\frac{π}{4}}\\ 0\end{array}}({sinx-acosx})dx=-\frac{{\sqrt{2}}}{2}$,则实数a等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | -1 | D. | $-\sqrt{3}$ |
分析 根据定积分的计算法则计算即可
解答 解:$\int_0^{\frac{π}{4}}{(sinx-acosx)dx=(-cosx-asinx)\left|{\begin{array}{l}{\frac{π}{4}}\\ 0\end{array}}\right.}=-\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{2}}}{2}a+1$,
∴-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$a+1=-$\frac{\sqrt{2}}{2}$,
∴a=$\sqrt{2}$,
故选B.
点评 本题考查了定积分的计算,属于基础题

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
3.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=lgx | B. | y=cosx | C. | y=|x| | D. | y=sinx |
19.设函数$f(x)=\sqrt{lnx+x+m}$,若曲线$y=\frac{1-e}{2}cosx+\frac{1+e}{2}$上存在(x0,y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
| A. | [0,e2-e+1] | B. | [0,e2+e-1] | C. | [0,e2+e+1] | D. | [0,e2-e-1] |
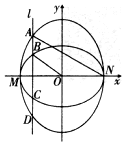 如图,已知椭圆C1的中心在原点O,长轴左、右端点M、N在x轴上,椭圆C2的短轴为MN,且C1、C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点纵坐标从大到小依次为A、B、C、D.
如图,已知椭圆C1的中心在原点O,长轴左、右端点M、N在x轴上,椭圆C2的短轴为MN,且C1、C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点纵坐标从大到小依次为A、B、C、D.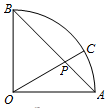 如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.
如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.