题目内容
现有一个由36名游客组成的旅游团到上海参观旅游，其中
是境外游客，其余是境内游客．在境外游客中有
持旅游金卡，在境内游客中有
持旅游银卡，其余游客都未持金、银卡．
（1）在该团中随机采访3名游客，求恰有1人持金卡且少于2人持银卡的概率；
（2）在该团的境内游客中随机采访3名游客，设采访到不持银卡人数为随机变量X，求随机变量X的分布列和均值．
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
（1）在该团中随机采访3名游客，求恰有1人持金卡且少于2人持银卡的概率；
（2）在该团的境内游客中随机采访3名游客，设采访到不持银卡人数为随机变量X，求随机变量X的分布列和均值．
考点：离散型随机变量的期望与方差,相互独立事件的概率乘法公式,离散型随机变量及其分布列
专题：概率与统计
分析：（1）由题意可得：境内游客有36×
人，其中境外游客中有27×
人持旅游金卡；境内游客有9人，在境内游客中有9×
=6持旅游银卡，有21人未持金、银卡．设事件A1表示“该团3人中，有1人持金卡，0人持银卡”，则P（A1）=
．设事件A2表示“该团3人中，有1人持金卡，1人持银卡”，则P（A2）=
．设事件B为“恰有1人持金卡且少于2人持银卡”，利用互斥事件的概率计算公式可得P（B）=P（A1）+P（A2）．
（2）X的可能取值为0，1，2，3．P（X=0）=
，P（X=1）=
，P（X=2）=
，P（X=3）=
，再由公式求即可．
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| ||||
|
| ||||||
|
（2）X的可能取值为0，1，2，3．P（X=0）=
| ||
|
| ||||
|
| ||||
|
| ||
|
解答：
解：（1）由题意可得：境内游客有36×
=27人，其中境外游客中有27×
=9人持旅游金卡；境内游客有9人，在境内游客中有9×
=6持旅游银卡，有21人未持金、银卡．
设事件A1表示“该团3人中，有1人持金卡，0人持银卡”，则P（A1）=
=
．
设事件A2表示“该团3人中，有1人持金卡，1人持银卡”，则P（A2）=
=
．
设事件B为“恰有1人持金卡且少于2人持银卡”，则P（B）=P（A1）+P（A2）=
+
=
．
（2）X的可能取值为0，1，2，3．P（X=0）=
=
，P（X=1）=
=
，P（X=2）=
=
，P（X=3）=
=
．
X的分布列为：
其EX=0×
+1×
+2×
+3×
=1．
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
设事件A1表示“该团3人中，有1人持金卡，0人持银卡”，则P（A1）=
| ||||
|
| 9 |
| 34 |
设事件A2表示“该团3人中，有1人持金卡，1人持银卡”，则P（A2）=
| ||||||
|
| 27 |
| 170 |
设事件B为“恰有1人持金卡且少于2人持银卡”，则P（B）=P（A1）+P（A2）=
| 9 |
| 34 |
| 27 |
| 170 |
| 36 |
| 85 |
（2）X的可能取值为0，1，2，3．P（X=0）=
| ||
|
| 5 |
| 21 |
| ||||
|
| 15 |
| 28 |
| ||||
|
| 3 |
| 14 |
| ||
|
| 1 |
| 84 |
X的分布列为：
| X | 0 | 1 | 2 | 3 | ||||||||
| P（X） |
|
|
|
|
| 5 |
| 21 |
| 15 |
| 28 |
| 3 |
| 14 |
| 1 |
| 84 |
点评：本题考查了古典概型的概率计算公式、互斥事件的概率计算公式、随机变量的分布列及其数学期望，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
读如图程序，当输出的值y的范围大于1时，则输入的x值的取值范围是（ ）
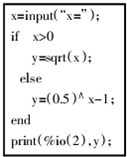
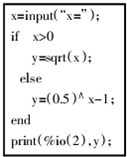
| A、（-∞，-1） |
| B、（1，+∞） |
| C、（-∞，-1）∪（1，+∞） |
| D、（-∞，0）∪（0，+∞） |
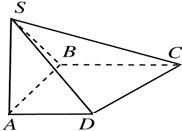如图所示，ABCD是直角梯形，∠ABC=90°，SA⊥底面ABCD，SA=AB=BC=1，AD=