题目内容
已知函数f(x)=aln(1+ex)-(a+1)x(其中a>0),点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3))从左到右依次是函数y=f(x)图象上三点,且2x2=x1+x3.
(1)证明:函数f(x)在R上是减函数;
(2)求证:△ABC是钝角三角形.
证明:(1)因为f(x)=aln(1+ex)-(a+1)x,所以f′(x)=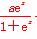 -(a+1)=
-(a+1)=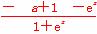 <0恒成立,所以函数f(x)在(-∞,+∞)上是单调减函数.
<0恒成立,所以函数f(x)在(-∞,+∞)上是单调减函数.
(2)据题意A (x1,f(x1)),B(x2,f(x2)),C(x3,f(x3))且x1<x2<x3,由(1)知f(x1)>
(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3))且x1<x2<x3,由(1)知f(x1)> f(x2)>f(x3),x2=
f(x2)>f(x3),x2=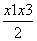 .所以
.所以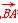 =(x1-x2,f(x1)-f(x2)),
=(x1-x2,f(x1)-f(x2)),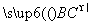 =(x3-x2,f(x3)-f(x2)),所以
=(x3-x2,f(x3)-f(x2)),所以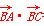 =(x1-x2)·(x3-x2)+[f(x1)-f(x2)]·[f(
=(x1-x2)·(x3-x2)+[f(x1)-f(x2)]·[f( x3)-f(x2)].
x3)-f(x2)].
 又x1-x2<0,x3-x2>0,f(x1)-f(x2)>0,f(x3)-f(x2)<0,所以
又x1-x2<0,x3-x2>0,f(x1)-f(x2)>0,f(x3)-f(x2)<0,所以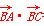 =(x1-x2)·(x3-x2)+[f(x1)-f(x2)]·[f(x3)-f(x2)]<0.
=(x1-x2)·(x3-x2)+[f(x1)-f(x2)]·[f(x3)-f(x2)]<0.
从而B∈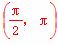 ,即△ABC是钝角三角形.
,即△ABC是钝角三角形.

练习册系列答案
相关题目
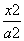 -
- =1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为e,过F2的直线与双曲线的右支交于A,B两点,若△F1AB是以A为直角顶点的等腰直角三角形,则e2=( ).
=1(a>0,b>0)的左、右焦点分别为F1,F2,离心率为e,过F2的直线与双曲线的右支交于A,B两点,若△F1AB是以A为直角顶点的等腰直角三角形,则e2=( ).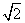 B.4-2
B.4-2 ,则输出s属于( )
,则输出s属于( )
 B、
B、 C、
C、  D、
D、
 >
> ”,假设内容应是______________.
”,假设内容应是______________.
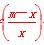 +f(m)<0,其中m∈R且m>0.
+f(m)<0,其中m∈R且m>0. …,观察
…,观察 ,…,则可归纳出
,…,则可归纳出 =( )
=( )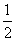 B.
B.
 C.
C. D.
D.
 为等比数列,
为等比数列, 是它的前
是它的前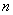 项和。若
项和。若 ,且
,且 与
与 的等差中项为
的等差中项为 则
则 ( )
( )