题目内容
已知f(x)是R上的单调函数,且对a∈R,有f(-a)+f(a)=0恒成立,若f(-3)=2.
(1)试判断f(x)在R上的单调性,并说明理由;
(2)解关于x的不等式f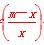 +f(m)<0,其中m∈R且m>0.
+f(m)<0,其中m∈R且m>0.
解析:(1)f(x)为R上的减函数.理由如下:
∵对a∈R,有f(-a)+f(a)=0恒成立,
∴f(x)是R上的奇函数.
∴f(0)=0.
∵f(x)是R上的单 调函数,f(
调函数,f( 0)<f(-3)=2,
0)<f(-3)=2,
∴f(x)为R上的减函数.
(2)由f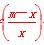 +f(m)<0,
+f(m)<0,
得f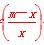 <-f(m)=f(-m),
<-f(m)=f(-m),
结合(1)得 >-m,
>-m,


练习册系列答案
相关题目
 命题
命题 则( )
则( ) B.
B. 
 D.
D. 
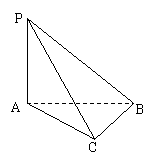
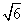 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为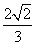 ,
,
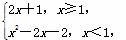
 D.c>a>b
D.c>a>b ≤4,求lg(x4y2)的取值范围.
≤4,求lg(x4y2)的取值范围. 则z=2x+3y的最小值为( )
则z=2x+3y的最小值为( )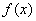 有两个零点
有两个零点 和
和 ,且
,且 ,函数
,函数 与
与 在区间[-1,1]上是增函数,求实数
在区间[-1,1]上是增函数,求实数 的取值范围.
的取值范围.