题目内容
20.有如下四个命题:①若a⊥α,b⊥α,则a∥b;
②空间中,若a⊥b,a⊥c,则b∥c;
③若a⊥α,b⊥a,则b∥a;
④若a⊥α,b∥a,b?β,则α⊥β,
其中为正确命题的是( )
| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
分析 由线面垂直的性质判断①;利用空间中直线与直线、直线与平面的位置关系判断②③;由线面垂直的判断及面面垂直的判定判断④.
解答 解:对于①,若a⊥α,b⊥α,由线面垂直的性质可得a∥b,故①正确;
对于②,空间中,若a⊥b,a⊥c,则c∥b或c与b相交或c、b异面,故②错误;
对于③,若a⊥α,b⊥a,则a与b相交或异面,故③错误;
对于④,若a⊥α,b∥a,则b⊥α,又b?β,则α⊥β,故④正确.
∴正确的命题是①④.
故选:B.
点评 本题考查命题的真假判断与应用,考查了空间中的线面关系,考查空间想象能力,是中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
11.化简$\frac{cos(2π+α)tan(π+α)}{{cos(\frac{π}{2}-α)}}$的结果为 ( )
| A. | 1 | B. | -1 | C. | tanα | D. | -tanα |
12.设函数f(x)在R上存在导函数f′(x),对于任意的实数x,都有f(x)=4x2-f(-x),当x∈(-∞,0)时,f′(x)+$\frac{1}{2}$<4x,若f(m+1)≤f(-m)+4m+2,则实数m的取值范围是( )
| A. | [-$\frac{1}{2}$,+∞) | B. | [-$\frac{3}{2}$,+∞) | C. | [-1,+∞) | D. | [-2,+∞) |
9.某城市理论预测2007年到2011年人口总数与年份的关系如表所示
(1)请根据上表提供的数据,求最小二乘法求出Y关于x的线性回归方程;
(2)据此估计2016年该城市人口总数.
| 年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(2)据此估计2016年该城市人口总数.
4.设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则( )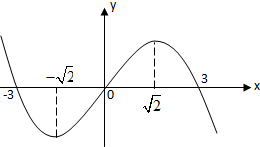

| A. | f(x)极大值为f($\sqrt{2}$),极小值为f(-$\sqrt{2}$) | B. | f(x)极大值为f(-$\sqrt{2}$),极小值为f($\sqrt{2}$) | ||
| C. | f(x)极大值为f(3),极小值为f(-3) | D. | f(x)极大值为f(-3),极小值为f(3) |