题目内容
4.设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则( )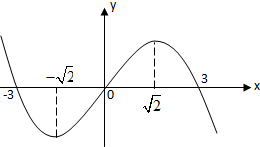
| A. | f(x)极大值为f($\sqrt{2}$),极小值为f(-$\sqrt{2}$) | B. | f(x)极大值为f(-$\sqrt{2}$),极小值为f($\sqrt{2}$) | ||
| C. | f(x)极大值为f(3),极小值为f(-3) | D. | f(x)极大值为f(-3),极小值为f(3) |
分析 观察图象知,x<-3时,f′(x)<0.-3<x<0时,f′(x)>0.由此知极小值为f(-3).0<x<3时,yf′(x)>0.x>3时,f′(x)<0.由此知极大值为f(3).
解答 解:观察图象知,x<-3时,y=x•f′(x)>0,
∴f′(x)<0.
-3<x<0时,y=x•f′(x)<0,
∴f′(x)>0.
由此知极小值为f(-3).
0<x<3时,y=x•f′(x)>0,
∴f′(x)>0.
x>3时,y=x•f′(x)<0,
∴f′(x)<0.
由此知极大值为f(3).
故选:C.
点评 本题考查极值的性质和应用,解题时要仔细图象,注意数形结合思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.有如下四个命题:
①若a⊥α,b⊥α,则a∥b;
②空间中,若a⊥b,a⊥c,则b∥c;
③若a⊥α,b⊥a,则b∥a;
④若a⊥α,b∥a,b?β,则α⊥β,
其中为正确命题的是( )
①若a⊥α,b⊥α,则a∥b;
②空间中,若a⊥b,a⊥c,则b∥c;
③若a⊥α,b⊥a,则b∥a;
④若a⊥α,b∥a,b?β,则α⊥β,
其中为正确命题的是( )
| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
9.已知函数f(x)=x2,则f(a-1)的值为( )
| A. | a2-1 | B. | a2-2a+2 | C. | a2-2a+1 | D. | a2-a+1 |