题目内容
设已知A、B为抛物线y2=2px(p>0)上两点,直线AB过焦点F,A、B在准线上的射影分别为C、D,给出下列命题:
(1)y轴上存在一点K,使得
•
=0;
(2)
•
=0;
(3)存在实数λ使得
=λ
;
(4)若线段AB中点P在准线上的射影为T,有
•
=0.
其中真命题的个数为( )
(1)y轴上存在一点K,使得
| KA |
| KF |
(2)
| CF |
| DF |
(3)存在实数λ使得
| AD |
| AO |
(4)若线段AB中点P在准线上的射影为T,有
| FT |
| AB |
其中真命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:根据抛物线方程,结合向量知识,即可得出结论.
解答:
解:(1)取AB⊥x轴,则A(
,p),F(
,0),
设K(0,a),则由(
,p-a)•(
,-a)=0,可得
-pa+a2=0,∴a=
,即(1)正确;
(2)由抛物线定义,知FA=CA,FB=DB,则∠ACF=∠AFC,∠BDF=∠BFD,则∠CFD=180°-∠AFC-∠BFD=180°-
(360°-∠FAC-∠FBD)=90°,∴
•
=0,正确;
(3)由(2),知△CXF与△FXD相似,即CX•DX=XF2=p2,
知AH=
,OX=
,得
=
,∴A、O、D共线,即(3)正确;
(4)设直线AB的倾斜角为α,知∠CFD为直角,即FT=
,而PT=
=
=
,有
=
=|cosα|,即AB⊥FT,∴
•
=0,正确.
故选:D.
| p |
| 2 |
| p |
| 2 |
设K(0,a),则由(
| p |
| 2 |
| p |
| 2 |
| p2 |
| 4 |
| p |
| 2 |
(2)由抛物线定义,知FA=CA,FB=DB,则∠ACF=∠AFC,∠BDF=∠BFD,则∠CFD=180°-∠AFC-∠BFD=180°-
| 1 |
| 2 |
| CF |
| DF |
(3)由(2),知△CXF与△FXD相似,即CX•DX=XF2=p2,
知AH=
| CX2 |
| 2p |
| p |
| 2 |
| AH |
| HO |
| OX |
| XD |
(4)设直线AB的倾斜角为α,知∠CFD为直角,即FT=
| CD |
| 2 |
| AC+BD |
| 2 |
| AF+BF |
| 2 |
| AB |
| 2 |
| FT |
| PT |
| CD |
| AB |
| FT |
| AB |
故选:D.
点评:本题考查抛物线方程与性质,考查学生分析解决问题的能力,综合性强.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
有5条线段长度分别为1,3,5,7,9,从中任意取出3条,则所取3条线段可构成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
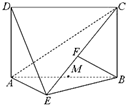 如图,四边形ABCD为矩形,∠AEB=
如图,四边形ABCD为矩形,∠AEB=